树的直径
直径的性质
- 任意两条直径必定相交
- 所有直径必交于一点
找直径
任意一个点出发,找出最远点,从最远点,在找到最远点,连起来就是直径(两次(dfs))。证明从略(反证法)。
P1099 树网的核
题目描述
设(T=(V,E,W))是一个无圈且连通的无向图(也称为无根树),每条边到有正整数的权,我们称(T)为树网(treebetwork),其中(V),(E)分别表示结点与边的集合,(W)表示各边长度的集合,并设(T)有(n)个结点。
路径:树网中任何两结点(a),(b)都存在唯一的一条简单路径,用(d(a,b))表示以(a,b)为端点的路径的长度,它是该路径上各边长度之和。我们称(d(a,b))为(a,b)两结点间的距离。
(D(v,P)=min{d(v,u)}), (u)为路径(P)上的结点。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网(T),直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距(ECC(F)):树网(T)中距路径(F)最远的结点到路径(F)的距离,即
(ECC(F)=max{d(v,F),v∈V})
任务:对于给定的树网(T=(V,E,W))和非负整数(s),求一个路径(F),他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过(s)(可以等于(s)),使偏心距(ECC(F))最小。我们称这个路径为树网(T=(V,E,W))的核(Core)。必要时,(F)可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
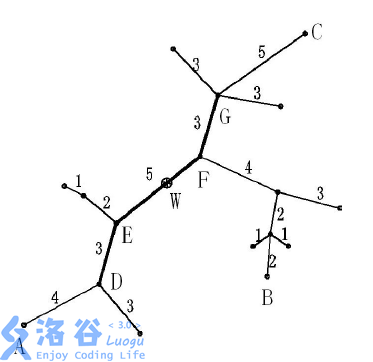
下面的图给出了树网的一个实例。图中,(A−B)与(A−C)是两条直径,长度均为(20)。点(W)是树网的中心,(EF)边的长度为(5)。如果指定(s=11),则树网的核为路径DEFG(也可以取为路径DEF),偏心距为(8)。如果指定(s=0)(或(s=1)、(s=2)),则树网的核为结点(F),偏心距为(12)。
输入输出格式
输入格式:
共(n)行。
第(1)行,两个正整数(n)和(s),中间用一个空格隔开。其中(n)为树网结点的个数,(s)为树网的核的长度的上界。设结点编号以此为(1,2,…,n)。
从第(2)行到第(n)行,每行给出(3)个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“(2~4~7)”表示连接结点(2)与(4)的边的长度为(7)。
输出格式:
一个非负整数,为指定意义下的最小偏心距。
输入输出样例
题解
由于某些原因,这条路径必定会在直径上,所以不妨找出直径然后暴力枚举。但是显而易见,对每一个点都进行暴力肯定是不行的,所以我们需要向一些办法。可以将直径当做一条链,考虑下图这样的情况:
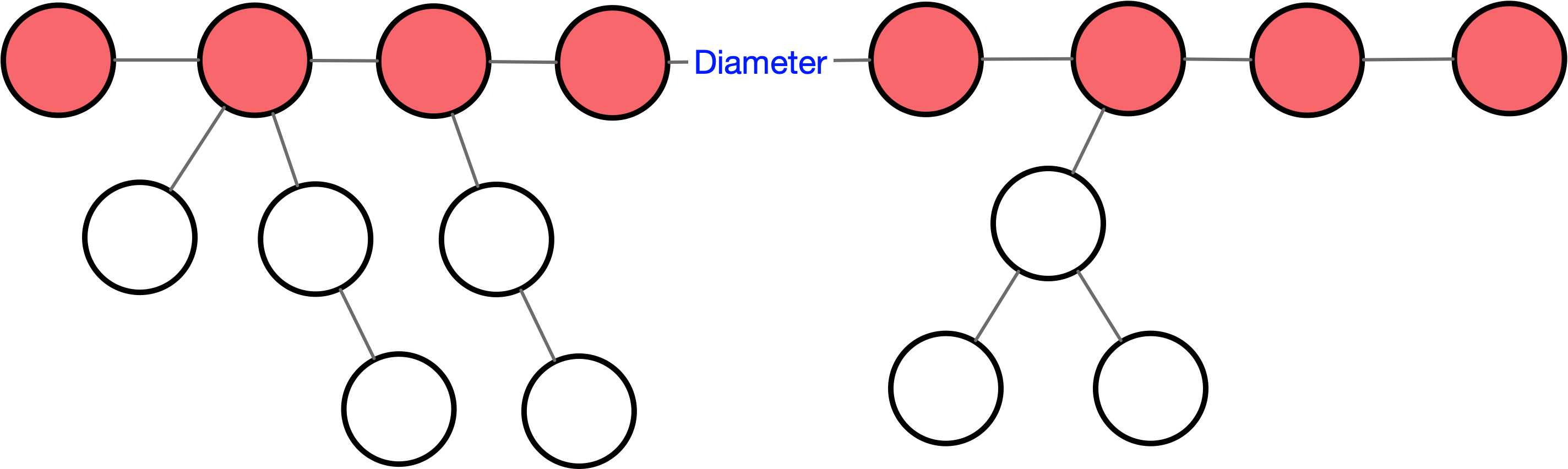
求出在这种情况之下的子树的最深深度,即为(secd[i]),其中(i)为直径上的点,之所以这么表示,因为这个深度是在一个节点所有子树当中第二深的深度,最深的深度(best[i])为直径所在的那颗子树的深度。
在这种情况下,可以在直径上选定一段(F)后,列出(ECC(F))的方程:
首先在找直径和求子树深度这些环节其实写法都是一样的,使用两次的(dfs),代码:
// x[u]: 高度,即u到顶的距离,secd[u]:最深子树(处直径外的子树),dim[u]:直径上u的后继
ll dfs_1(ll u, ll p) {
ll alpha = u;
for (ll e = h[u]; e != 0; e = g[e].next) {
ll v = g[e].to;
if (v != p) {
f[v] = f[u] + g[e].w;
ll a = dfs_1(v, u);
if (f[a] > f[alpha])
alpha = a;
}
}
return alpha;
}
void dfs_2(ll u, ll p) {
for (ll e = h[u]; e != 0; e = g[e].next) {
ll v = g[e].to;
if (v != p) {
x[v] = x[u] + g[e].w;
dfs_2(v, u);
ll newd = g[e].w + maxd[v];
if (newd >= maxd[u]) {
secd[u] = maxd[u];
maxd[u] = newd;
dim[u] = v;
} else if (newd > secd[u]) {
secd[u] = newd;
}
}
}
}
后面的暴力判断哪一段最佳则可以有两种做法:
- RMQ:
namespace RMQ {
void init() {
for (ll i = 1; i <= n; i ++) d[i][0] = i;
for (ll j = 1; (1 << j) <= n; j ++)
for (ll i = 1; i + (1 << j) - 1 <= n; i ++) {
ll x = d[i][j - 1], y = d[i + (1 << (j - 1))][j - 1];
d[i][j] = secd[Z[x]] > secd[Z[y]] ? x : y;
}
}
ll query(ll l, ll r) {
ll k = log2(r - l + 1);
ll x = d[l][k], y = d[r - (1 << k) + 1][k];
return secd[Z[x]] > secd[Z[y]] ? x : y;
}
}
int main() {
cin >> n >> L;
for (ll i = 1; i < n; i ++) {
ll u, v, w; cin >> u >> v >> w;
add_edge(u, v, w); add_edge(v, u, w);
}
ll a = dfs_1(1, 0);
dfs_2(a, 0);
ll k = 0;
for (ll p = a; p != 0; p = dim[p])
Z[++ k] = p;
ll diameter = x[Z[k]];
RMQ::init();
ll ans = 1LL << 62;
for (ll i = 1, j = 1; i <= k; i ++) {
ll u = Z[i], v = Z[j];
while (j + 1 <= k) {
ll v_1 = Z[j + 1];
if (x[v_1] - x[u] <= L) {
v = v_1;
j ++;
} else break;
}
ll ecc = secd[Z[RMQ::query(i, j)]];
ecc = max(ecc, x[u]);
ecc = max(ecc, diameter - x[v]);
ans = min(ans, ecc);
}
cout << ans << endl;
return 0;
}
- 单调队列:
void inc(ll &i) {
i ++;
if (head <= tail && q[head] == Z[i - 1]) {
head ++;
}
}
void adv(ll &j) {
j ++;
while (head <= tail) {
int last = q[tail];
if (secd[last] < secd[Z[j]]) {
tail --;
} else break;
}
tail ++;
q[tail] = Z[j];
}
int main() {
cin >> n >> L;
for (ll i = 1; i < n; i ++) {
ll u, v, w; cin >> u >> v >> w;
add_edge(u, v, w); add_edge(v, u, w);
}
ll a = dfs_1(1, 0);
dfs_2(a, 0);
ll k = 0;
for (ll p = a; p != 0; p = dim[p]) {
Z[++ k] = p;
}
ll diameter = x[Z[k]];
ll ans = 1LL << 62;
// 单调队列,其中inc(i)和adv(j)为对i,j分别加一,但是加的过程中需要调整单调队列的队首和队尾的指针,所以写成void
for (ll i = 1, j = 1; i <= k; inc(i)) {
ll u = Z[i], v = Z[j];
while (j + 1 <= k) {
ll v_1 = Z[j + 1];
if (x[v_1] - x[u] <= L) {
v = v_1;
adv(j);
} else break;
}
ll ecc = max(secd[q[head]], x[u]);
ecc = max(ecc, diameter - x[v]);
ans = min(ans, ecc);
}
cout << ans << endl;
return 0;
}
HDU-2196-Computers
题目大意
对于一张给定的图(是树),有边权,输出每个点的到树上末梢的最远距离。
题解
这道题可以通过找出直径,每个点的最远距离就是这个点对于直径两个点的距离中较大的那个,可以很快的通过(3)遍(dfs)解决。
但是由于这是一道(HDU)的题,还是multiple test cases,怎么死的都不知道,还需要额外的优化,所以这里用的是(vector)建图,删的时候直接(erase())就可以了。
代码:
#include <iostream>
#include <cstring>
#include <stdio.h>
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
const int maxn = 10005;
int val[maxn], end_of_diameter, max_length, ans[maxn];
int n;
struct node {
int to; int w;
node(int to, int w) : to(to), w(w) {}
};
vector < vector <node> > g;
// 这里开len可以省掉一个数组,每次dfs开始时计算答案
void DFS(int u, int fa, int len) {
if (len >= max_length) {
max_length = len; end_of_diameter = u;
}
for (int i = 0; i < g[u].size(); i ++) {
int v = g[u][i].to;
if (v == fa) continue;
int w = g[u][i].w;
DFS(v, u, len + w);
ans[v] = max(ans[v], len + w); // 这样做可以将两个数组化为一个数组
}
}
void init() {
g.clear();
g.resize(n + 2);
memset(ans, 0, sizeof(ans));
max_length = 0;
end_of_diameter = 0;
}
int main() {
int v, w;
while (scanf("%d", &n) != EOF) {
init();
for (int i = 2; i <= n; i ++) {
scanf("%d%d", &v, &w);
g[i].push_back({v, w});
g[v].push_back({i, w});
}
DFS(1, -1, 0);
DFS(end_of_diameter, -1, 0);
DFS(end_of_diameter, -1, 0);
for (int i = 1; i <= n; i ++)
printf("%d
", ans[i]);
}
return 0;
}