1.数据流
数据流的产生:实时监控系统、气象卫星遥感、网络通信量监测和电力供应网等
数据流的特点:海量的(massive)、时序的(temporally ordered)、快速变化的和潜在无限、高维的(potentially infinite)。
数据流挖掘的特点---挑战:
(a)数据是海量的,不可能在内存及硬盘上存储整个流数据集。
(b)单次线性扫描(单遍扫描)(single pass)的过程;数据元素只能按其流入顺序依次读取一次,随机访问是不现实的。
(c)数据流是持续变化的,所以不可能看到数据流的中的每一个数据元素(data point),我们只能通过分析部分数据元素来做出决策。
(d)大多数应用要求及时响应,对时间复杂度、空间复杂度要求很高,并且挖掘应该是一个连续、在线的过程。
(e)数据流往往是高维的(High-Dimensional),不同的领域的数据流挖掘面临的挑战也不一样。
(f)时间局部性(temporal locality),过去的历史数据或许与将来的关系越来越小,只与当前时间点很相关
(g)可扩展性(scalability)
所以:数据流算法经常采用精度换时间的方法,尽量在对数据的一次访问中获得较优的解.一般来说,数据流算法是不可回溯的;其次,数据流算法有很多特点,一些数据库应用中常用的操作在数据流中都是不可行的.如,Sort,Max,Count 等操作。
1.2数据流模型
数据流中的数据项 x 1 , …, xi , …, xn 依次按下标顺序到达 ,它们描述了一个信号 A。
1.2.1按 xi描述信号 A的方式 ,数据流模型可分为以下几类:
(1)时序( Time Series)模型:A [ i ] = xi ,用来描述时间序列数据。此时 ,数据流中的每个数据项都代表一个独立的信号。
(2)现金登记 (Cash Register)模型:令 xi = ( j,Ii ) ,且 Ii≥0,则 Ai [ j ] =Ai-1 [ j ] + I i。此时 ,数据流中的多个数据项增量式地表达一个 A [ j ]。
(3)十字转门( Turnstile)模型:令 xi = ( j,Ui) ,则Ai[ j ] =Ai -1 [ j ] +Ui。其中 , Ui可为正数 ,也可为负数。此时 ,数据流中的多个数据项表达一个 A [ j ]。A[ j ]随着数据的流入 ,可能会增加 ,也可能会减小。
1.2.2按照算法处理数据流时所采用的时序范围 ,数据流模型可分为以下几类:
(1)快照模型 ( Snapshot Model) :处理数据的范围限制在两个预定义的时间戳之间。
(2)界标模型 (Landmark Model) :处理数据的范围从某一个已知的初始时间点到当前时间点为止。
(3)滑动窗口模型 (Sliding Window Model) :处理数据的范围由某个固定大小的滑动窗口确定 ,此滑动窗口的终点永远为当前时刻。其中 ,滑动窗口的大小可以由一个时间区间定义 ,也可以由窗口所包含的数据项数目定义。
2.数据流聚类基本知识
2.1聚类方法
聚类(Clustering)是指对一个数据对象集合,将其中相似的对象划分为一个或多个组(称为“簇”,Cluster)的过程。同一个簇中的元素是彼此相似的,而与其它簇中的元素相异。
考虑时间局部性:基于流数据快照的方法(snapshot-based methods), 基于衰减的技术(decay-based techniques), 滑动窗口方法windowing
数据流聚类要求:适合于数据流模型的、仅使用有界内存和有限处理时间的单遍扫描数据的高效聚类方法。
一个好的数据流聚类算法应该具备的3个要求:
(a)对已发现的簇提供一个简洁的表示方法(representation);
(b)对新的数据元素的处理应该是增量式的方式(incremental processing),并且应该它是快速的;
(c)有清晰而快速地孤立点检测(outlier detection)的能力。
2.2支撑技术
基于数据的技术(Data-based Techniques)
抽样(Sampling)
使用水库抽样(reservior sampling)的技术来解决这个问题:在“水库”中维护s个候选的样本,形成目前看到的流的随机样本集,随着数据流的流动,新的数据元素都有一定的概率替代水库中的元素。
梗概(Sketching)
梗概是一个将数据流中的数据向量做一个随机投影的过程。它建立这些分布向量(如直方图)的小空间汇总。梗概广泛用于不同数据流的比较和聚集查询。梗概是对精度和存储空间进行折衷的极佳范例,精度问题是它的主要缺陷。
大纲数据结构(Synopsis Data Structure)
通过应用概要技术(summarization techniques),生成的比当前数据流小得多的数据结构。它是当前数据流的概要描述。已经被提出的概要技术包括:小波分析、直方图(histogram)和频率矩(frequency moment)等。
大纲数据结构不可能表示出原数据流的所有特性,使用大纲数据结构只能得到一个近似结果。
聚集运算(Aggregation)
聚集运算试图通过计算一些统计度量,诸如平均数和方差等来概括当前的数据流。不过类似所有统计学的方法,它不适合速率高度摇摆和分布式的数据流
2.3基于任务的技术(Task-based Techniques)
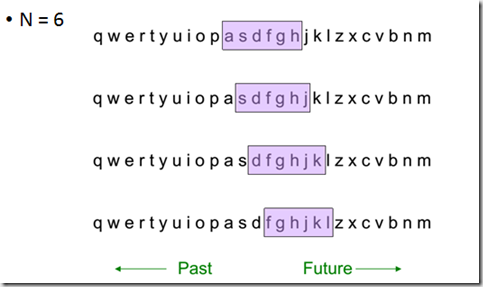
滑动窗口(Sliding Window)
滑动窗口模型基于这样一个事实:“用户对于最近的数据更感兴趣。”这样,我们可以对少量的近期数据做细节分析,而对大量的历史数据,仅仅给出一个概要试图。这样,只需存储小的数据窗口,减少了对内存的需求。缺陷是要求用户预先指定窗口的尺寸,而在很多应用中,窗口的大小不可能事先知道。
衰减函数(Fading Function)
另一种强调近期数据的重要性、消减历史数据对计算结果影响的方法是衰减因子和衰减函数。数据元素在参与计算前,先经过衰减函数的作用。因此,每个数据元素对最终结果的影响将随着时间的推移逐渐减小。一种常用的衰减函数形式为指数形式,例如 Den-Stream算法使用的衰减函数为:
倾斜时间框架(Titled Time Frame)
滑动窗口和衰减函数都只能在单一时间维的窗口上得到计算结果。然而,很多应用要求在不同的时间粒度层上进行分析和挖掘。比如,用户通常对细粒度层上的当前变化感兴趣,而在粗粒度层上对长期变化感兴趣。最近的数据在最细的粒度层上记录和运算,较久远的数据在较粗的粒度上记录和运算。
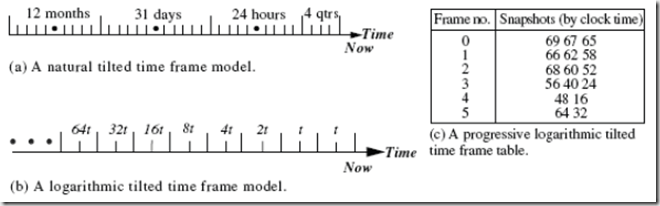
三种倾斜时间框架模型:自然倾斜时间框架模型(natural)、对数尺度倾斜时间框架模型(logarithmic scale)和渐进对数时间框架模型(progressive logarithmic)。如图1
图1 倾斜时间框架的三种模式
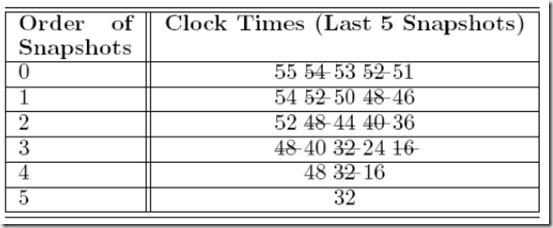
Aggarwal等在文献[8]中提出的CluStream聚类算法就是基于一种称为Pyramidal Time Frame的渐进对数倾斜时间框架模型,如表1所示
表1 金字塔时间框架模型(An example of snapshots stored for α=2)
距离当前越近的时间戳,快照存储的密度就越高。并且,渐进对数时间框架维护了一个替代算法,使新的流数据到来时能插入正确的时间粒度层,以替代最老的数据。
不同时间粒度层中的数据存在重叠(表中划横线的数据即为重叠数据)。并且可知,重叠数据为每层上能被αi整除的数据。
3.数据流聚类算法
3.1基于划分的方法---STREAM算法
S. Guha 等人在提出了基于K-Means 的STREAM 算法,使用质心(中心点,中位数)和权值(类中数据个数)表示聚类。STREAM算法采用批处理方式,每次批处理的数据点个数受内存大小的限制。对于每一批数据Bi,STREAM算法对其进行聚类,得到加权的聚类质心集Ci。
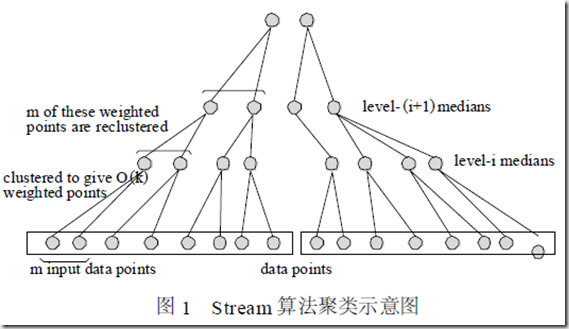
STREAM算法采用分级聚类的方法,如图1 所示,首先对最初的m 个输入数据进行聚类得到O(K)个1 级带权质心,然后将上述过程重复m/O(K) 次,得到m 个1 级带权质心,然后对这m 个1 级带权质心再进行聚类得到O(K) 个2级带权质心;同理,每当得到m 个i 级带权质心时,就对这些质心进行一次聚类得到O(K) 个i+1 级带权质心;重复这一过程直到得到最终的O(K)个质心。对于每个第i+1 级带权质心而言,其权值是与它对应的i 级质心的权值之和。
---------------------------------------------------------------------------------------------------------------------------
STREAM算法聚焦于解决k-中位数问题(k-medians),即把度量空间中的n个数据点聚类成k个簇,使得数据点与其簇之间的误差平方和(SSQ)最小。
STREAM算法处理m个数据点的桶中的数据流,桶的大小与内存相符。算法把每个桶的数据点分成k个簇,并且仅仅保留k个簇中心点(而丢弃其余的数据)来汇总桶中的所有数据。每个中心点的权(weight)为该簇中数据点的个数。随着数据流的流入,这个过程不断地被重复,每次处理的数据个数为m个。
此外,STREAM算法采用分级聚类的技术,使用Local Search算法改进了k-平均算法(k-means),使“k”更灵活:在算法的中间步骤中,簇的个数不再是一个固定的值,而是一个更合理的值,仅仅在算法结束时趋向于k。得到了更好的性能和更高质量的结果簇。
如上所述,STREAM算法实现了单次扫描,时间复杂度为O(kn)。
优点和缺点:
STREAM算法与传统数据的聚类算法相比(与BIRCH相比较),有更好的性能,并能产生更高质量的聚类结果。
(1)STREAM算法没有考虑数据流的演变,即算法没有给予最近的数据较大的权重。聚类的结果可能受控于过期的数据点。(2)STREAM算法更趋近与一个批处理的过程,无法给出一个anytime的回应,即算法无法在任意时刻给出当前数据流的聚类结果。(3)STREAM的不足还包括无法给出不同时间粒度的聚类结果等等。
3.2基于层次的方法---CluStream
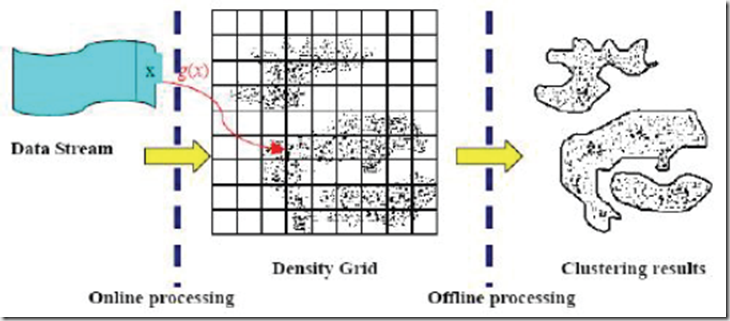
CluStream是一个数据流聚类的处理框架,它把聚类过程分为两个部分:联机的微聚类(micro clustering)和脱机的宏聚类(macro clustering)。CluStream的提出的这个两阶段处理框架被许许多多后来的数据流聚类算法所采用和遵循。
CluStream是一个数据流的聚类分析框架。CluStream算法解决了STREAM算法的两个问题。即它是增量式(incremental)的聚类算法,在每个数据项到来时进行处理,能给出anytime的回应;并且,它使用Pyramidal时间框架,能给出不同时间粒度的聚类结果。这对于希望分别考察诸如上周、上月以及去年的聚类分析结果的用户意义重大!
联机部分使用微簇(micro cluster)计算和存储数据流的汇总统计信息,实现增量的联机聚类查询;脱机部分则进行宏聚类(macro clustering),利用Pyramidal时间框架提供用户感兴趣的不同时间粒度上的聚类结果。CluStream的这个两阶段处理框架被许许多多后来的数据流聚类算法所效仿和采纳。
由BIRCH中CF的可加减性,不难推导出CluStream中的聚类特征的可加减性。籍此,CluStream算法成为一个增量式的处理过程。
联机的微簇维护过程由初始化和更新阶段组成:首先初始化q个微簇M1…Mq ,q根据内存的情况取尽可能大的值,q个微簇根据当前数据的统计信息用k-means算法得到。然后,更新微簇。每个新数据点根据是否落在某个微簇的边界之内,选择加入某个微簇或者新建一个微簇。前者根据可加性被已存在的微簇“吸收”,后者则需要删除一个最近最少用的微簇或者合并存在的微簇以保持q值不变。
脱机部分实现用户指导的宏聚类和聚类演变分析。宏聚类提供用户要求的不同时间粒度的聚类结果;聚类演变分析考察聚类结果如何随时间变化。通过Pyramidal时间框架和聚类特征的可加减性,这两点都不难实现。前者根据当前时间tc和用户指定的时间范围h,在Pyramidal时间框架中找到t时刻的快照S(t)和(tc-h)时刻的快照S(tc-h),相减得到(tc-h)到tc之间生成的微簇集N(tc, h)。N(tc, h)即是加权虚拟点集。然后用STREAM算法进行聚类,得到h时间范围内的数据流聚类结果。
聚类演变分析(Evolution Analysis)告诉用户在哪些数据点在t1时刻的簇中出现而在t2时刻的簇中消失,哪些数据点在两个时刻的簇中都存在。给定t1 、t2和h,计算出N(t1, h)和N(t2, h)。通过比较N(t1, h)和N(t2, h),就不难回答上述的问题。
CluStream通过使用倾斜时间框架,保存了数据流演变的历史信息,在数据流变化剧烈时仍可以产生高质量的聚类结果,并且提供了丰富的功能。但是,它没有考虑历史数据的衰减问题,即没有体现出近期数据的重要性。此外,当被应用于高维数据流的聚类时,CluStream算法往往表现不佳。
HPStream基于“众多数据流天生就是高维的。”这个事实,通过引入投影技术(project clustering)和衰减簇结构(fading cluster structure),来更好地支持高维数据流的聚类分析。CluStream和HPStream是两种被广泛认可、并且十分流行的数据流聚类算法。
HPStream针对高维数据流,较之CluStream主要做了如下改进:首先,HPSream引进了投影聚类技术(projected clustering)来处理高维的数据流,这比STREAM和CluStream中对所有相关维做全维聚类(full dimensional clustering)要高效和合理。其次,与CluStream在整个数据流上计算微簇不同的是,HPStream使用衰减簇结构(fading cluster structure)来保存历史数据。衰减簇结构使用衰减因子,随着时间的推进,不断衰减历史数据对当前聚类结果的影响,更好地将当前数据和历史数据集成起来。
3.3基于密度的算法---DenStream
面向数据流的基于密度的聚类算法DenStream。它采用CluStream算法中提出的两阶段处理框架,并引入了潜在簇结构和孤立点簇结构。实际上,当聚类请求到达时,DenStream仍然采用DBSCAN算法来得到最后的聚类结果。
扩展划分和层次的方法,诸如STREAM、CluStream和HPStream等算法的主要问题在于:它们仅仅对球形的数据流进行聚类分析时表现良好,但由于采用距离度量,它们不能很好地处理任意形状的数据流。
DenStream算法扩展了传统数据集聚类算法中基于密度的方法DBSCAN,着眼于处理任意形状的数据流聚类问题。同时,它强调了孤立点检测问题,将孤立点与正常数据元素区分开来。
DenStream算法沿袭了CluStream的处理框架,把聚类分析的过程划分为联机和脱机两个部分。
在联机部分中,算法维护了两类微簇结构:潜在微簇(p-micro-cluster)和孤立点微簇(o-micro-cluster),这两个微簇结构的不同之处仅仅在于其约束条件——密度小于某个阈值的簇被当作孤立点簇,而密度超过该阈值的簇被视为潜在微簇。当一个新的数据点到来时,算法(1)首先试图将它合并到其最邻近的p-micro-cluster中;若失败,则(2)试图将其合并到最邻近的o-micro-cluster中去。若合并成功,检测该o-micro-cluster的密度是否大于阈值,若是,则将该o-micro-cluster转换为p-micro-cluster;(3)如果仍然无法找到最邻近的o-micro-cluster,则新建一个o-micro-cluster来容纳该数据点。该子算法的流程见图4。
对于脱机部分,当用户的聚类要求到来时,DenStream算法先忽略密度不足够的两类微簇,然后使用DBSCAN算法,对当前的p-micro-cluster和o-micro-cluster进行处理,得到聚类结果并返回。
3.4基于网格的方法---D-Stream
D-Stream就是一个基于网格和密度的数据流聚类算法。它使用密度网格(Density grid),基于密度和网格产生高质量的聚类结果。
D-Stream算法是一个基于密度和网格的算法。与DenStream算法一样,D-Stream算法也着力解决对任意形状的数据流聚类问题、强调了孤立点探测,并且依据密度来判断聚类。所不同的是,它是一个基于网格的算法,使用密度网格(Density Grid)结构。
D-Stream算法同样分为联机和脱机两个部分。联机部分将接受到的每个数据元素映射到某个网格中,而脱机部分计算这些网格的密度,并且基于密度将这些网格进行聚类。
使用密度网格来进行聚类的过程如图5所示。联机部分持续地读入新的数据元素,并将多维的数据元素映射到多维空间内对应的离散的密度网格中,同时更新密度网格的特征向量。脱机部分在每隔一个时间隙(gap time)后动态地调整当前的簇。初始簇在第一个时间隙后形成,此后算法周期性地移除零星的簇,并调节已经生成的簇。通过使用网格结构,我们无需保留大量的原始数据,而仅仅需要对网格进行操作。
由于联机部分仅仅是将数据元素映射到相应的网格中,而无需计算距离或权值,D-Stream相比不使用网格的算法更高效。并且它的可扩展性更好,即算法不会随着数据量的增大而变慢。但是,D-Stream算法的问题是对于高维数据流,所需要的网格的数量可能会非常大。
3.5其他方法
基于模型的方法试图为数据集假定一个数学模型,诸如统计学模型和神经网络模型[1]。基于模型的方法如EM算法(Expectation-Maximization)、COBWEB等。
利用回归分析实现数据流聚类的算法CFR
Domingos等扩展了机器学习中的算法,提出的基于Hoeffding界和k-平均算法的VFKM算法(Very Fast K-Means);Gaber等提出的基于AOG(Algorithm Output Granularity)的面向传感器网络中数据流的LWC算法(Lightweight Clustering)等
几乎所有2003年以后的数据流聚类算法都实现了增量式的处理方式,可以满足用户anytime的聚类请求。E-Stream算法实现对数据流演化的表示方式。CluStream算法框架实现了数据流的聚类演变分析,这在网络入侵检测中非常有用,可以识别网络上新的攻击类型[1]。通过使用倾斜时间框架,聚类算法可以提供不同时间粒度的聚类结果。而使用衰减函数,近期的数据得到了更大的重视。几乎所有的两阶段聚类算法都可以支持用户的联机聚类请求。
为了处理高维数据流,HPStream算法使用了投影聚类技术。而大多数基于密度及网格的方法都能对任意形状的数据流进行聚类分析。