【LeetCode】105 & 106. Construct Binary Tree from Inorder and Postorder Traversal

题目：

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

提示：

题目要求通过一颗二叉树的中序遍历及后续遍历的结果，将这颗二叉树构建出来，另外还有一个已知条件，所有节点的值都是不同的。

首先需要了解一下二叉树不同遍历方式的定义：

• 前序遍历：首先访问根结点，然后遍历左子树，最后遍历右子树；
• 中序遍历：首先遍历左子树，然后访问根结点，最后遍历右子树；
• 后序遍历：首先遍历左子树，然后遍历右子树，最后访问根结点。

以下图显示的二叉树为例：

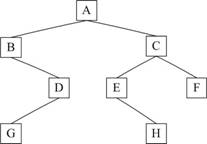
该二叉树的前序遍历为：ABDGCEHF

              中序遍历为：BGDAEHCF

              后序遍历为：GDBHEFCA

了解了不同遍历方式的定义，我们就可以想办法解决这个问题了。对于这题，我们提供两种不同的解决方法。

方法一：

方法一是比较简单直观的一种，许多有关二叉树的题目实际上都可以用递归的方法去解决，这题也不例外，先上代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return create(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
    }
    
    TreeNode* create(vector<int>& inorder, vector<int>& postorder, int is, int ie, int ps, int pe) {
            if (ps > pe || is > ie) return nullptr;
            TreeNode* node = new TreeNode(postorder[pe]);
            int pos;
            for (int i = is; i <= ie; ++i) {
                if (inorder[i] == node->val) {
                    pos = i;
                    break;
                }
            }
            node->left = create(inorder, postorder, is, pos - 1, ps, ps + pos - 1 - is);
            node->right = create(inorder, postorder, pos + 1, ie, pe - ie + pos, pe - 1);
            return node;
    }
};

我们创建一个叫做create的递归函数，该函数接受六个参数，其含义分别是：

• vector<int>& inorder ：中序遍历的结果

• vector<int>& postorder ：后序遍历的结果

• int is ：中序遍历开始的索引

• int ie ： 中序遍历结束的索引

• int ps ：后序遍历开始的索引

• int pe　：后序遍历结束的索引

借助create函数，二叉树的每一个子树都会变成一个类似的子问题，对这些子问题进行递归，就能完成树的构建。下面我们分析一下create函数：

首先是终止条件的判断：

if (ps > pe || is > ie) return nullptr;

很好理解，起始位置的索引如果大于终止位置的索引，那么就返回一个空节点。

如果没有满足终止条件，那么我们就先找出这个子问题的根节点，回忆后序遍历的定义，树的根节点是最后才会被遍历到的，因此我们可以这样构建根节点：

TreeNode* node = new TreeNode(postorder[pe]);

而对于中序遍历来说，根节点会在当中的某一个位置，因此我们用一个for循环去定位根节点在中序遍历中的位置：

int pos;
for (int i = is; i <= ie; ++i) {
    if (inorder[i] == node->val) {
        pos = i;
        break;
    }
}

相应的位置存储在了pos这一变量中。有了这一位置，我们就可以进一步将问题划分成左右两个子问题了，这也是该算法的核心，其难点在于确定中序遍历与后序遍历的起始位置索引和结束位置索引。

比较好判断的是中序遍历，由于中序遍历的顺序为“左根右”，因此小于pos的都属于左侧子树，pos为根节点，大于pos的为右侧子树，因此对于左子树的开始和终止索引分别为：is和pos - 1；而右子树的开始和终止索引分别为：pos + 1和ie。

比较难判断的后序遍历，我们先看左子树。毫无疑问，由于后序遍历的顺序为“左右根”，对于左子树，后序遍历的开始索引依然是ps，但是结束位置会有变化。由于中序遍历在访问到根节点前会把左侧子树的节点都遍历完，而后序遍历同样也是一开始遍历左侧子树，直到遇到根节点的左子节点，再去遍历右侧子树，所以对于左侧子树这一子问题，后序遍历的节点个数可以直接根据中序遍历获得，那么中序遍历在左子树上遍历了多少个节点呢？其实就是结束位置的索引和开始位置索引的差：pos - 1 - is，因此，后序遍历在左子树上终止位置的索引为：ps + pos - 1 - is。

这里很容易犯的一个错误是忽略了“- is”这一项，因为我们很容易直观地觉得既然pos对应了根节点，那么左侧子树的节点个数就是pos - 1，但是如果我们现在是在解决根节点右侧子节点的左子树呢？此时is可就不是0了，因此不要忘记减去它。

node->left = create(inorder, postorder, is, pos - 1, ps, ps + pos - 1 - is);

那么左侧子树搞定了之后，我们再看右侧子树，后序遍历右侧子树的结束位置很好判断，因为pe对应了根节点，所以右侧子树的结束位置就是pe - 1（对应了根节点的右子节点），那么起始位置应该怎么计算呢？和左侧子树的问题一样，已知结束的位置，我们只要借助中序遍历计算出遍历节点的个数就可以很好判断出开始的位置是多少了。那么中序遍历在右侧子树上回遍历多少个节点？类似的，就是中序遍历的结束位置ie与开始位置pos + 1的差：ie - pos - 1，所以，后序遍历的开始位置为：pe - 1 - (ie - pos - 1) = pe - ie + pos。

node->right = create(inorder, postorder, pos + 1, ie, pe - ie + pos, pe - 1);

至此递归函数也分析的差不多了。

虽然递归法的逻辑比较清晰，可以帮助我们更快地理解问题的本质，但是其时空复杂度都不太理想。如果希望能够让算法更加高效，我们就需要将它替换成迭代版本，这就是下面将要提到的方法二。

方法二：

想必大家都知道只要利用stack这一数据结构，就可以将递归算法转变成迭代循环。

这里将树节点的指针存储在stack中，更具体的说，stack存储的是所有还没有处理左节点的节点指针。一开始先把根节点push到stack中，同时将后序遍历的最后一个元素（对应根节点），pop出来：

stack<TreeNode*> s;      
TreeNode *root = new TreeNode(postorder.back());
s.push(root);
postorder.pop_back();

然后就是一个循环，去迭代地构建出二叉树。在循环中，我们主要依靠中序遍历，每次查看中序遍历的最后一个元素，即最右侧的节点，和当前栈顶元素的值是否一样。如果不一样的话，那么就说明当前栈中所存储的节点，还没有到最右下角的节点，那么这个时候，我们就把后序遍历中最后一个元素继续压入到栈中，并且把该元素从后序遍历里面pop出来。

TreeNode *p = new TreeNode(postorder.back());
postorder.pop_back();
s.top()->right = p;
s.push(p);

可以想象一下，除非这个二叉树一个右侧子节点都没有，不然刚开始的几次循环一定是会做上述压栈操作的。

如果中序遍历的最后一个元素和当前栈顶元素的值一样，此时我们将该元素从栈中取出，同时相应元素出栈，并把中序遍历的最后一个元素也剔除：

TreeNode *p = s.top();
inorder.pop_back();
s.pop();

如果这个时候存放中序遍历的vector空了，那么我们就达到了终止条件，此时跳出循环：

if (!inorder.size()) break;

如果没有结束，那么此时对于该栈顶元素对应的节点而言，可能会有两种情况：

• 第一种情况：这个节点没有左子节点；
• 第二种情况：这个节点有左子节点。

对于第一种情况，由于该节点没有左子节点，因此若将该节点从中序遍历的末尾剔除后，此时中序遍历的最后一个元素应该与当前栈顶元素的值相等（记住之前已经将上一个栈顶元素出栈了）。由于没有左节点，而右节点又已经构建好了（之前的“s.top()->right = p;”）因此我们继续循环。

对于第二种情况，我们就需要把该节点的左节点构建出来，那么左节点的值是多少呢？回忆后序遍历“左右根”的顺序，由于我们现在是从后往前做，即“根右左”，因此此时后序遍历的最后一个元素就是该节点的左节点。因此我们把这个节点的左节点构建好后，将其左节点压栈。

下面贴出整个代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size() == 0) return nullptr;
        TreeNode *p, *root;
        stack<TreeNode*> s;
        
        root = new TreeNode(postorder.back());
        s.push(root);
        postorder.pop_back();
        
        while(true) {
            if (inorder.back() == s.top()->val) {
                p = s.top();
                inorder.pop_back();
                s.pop();
                if (!inorder.size()) break;
                if (s.size() && inorder.back() == s.top()->val) continue;
                p->left = new TreeNode(postorder.back());
                postorder.pop_back();
                s.push(p->left);
            } else {
                p = new TreeNode(postorder.back());
                postorder.pop_back();
                s.top()->right = p;
                s.push(p);
            }
        }
        return root;
    }
};

以上就是该题的完整分析。在LeetCode上还有一道类似的题目，可以作为练习，题目如下：

题目：

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

两种方法对该问题都适用，这里就不再一一分析了，直接贴出答案。

方法一：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return create(preorder, inorder, 0, preorder.size()-1, 0, inorder.size()-1);
    }
    
    TreeNode* create(vector<int>& preorder, vector<int>& inorder, int ps, int pe, int is, int ie) {
        if(ps > pe) {
            return nullptr;
        }
        TreeNode *root = new TreeNode(preorder[ps]);
        int pos;
        for (int i = is; i <= ie; ++i) {
            if (inorder[i] == root->val) {
                pos = i;
                break;
            }
        }
        root->left = create(preorder, inorder, ps + 1, ps + pos - is, is, pos - 1);
        root->right = create(preorder, inorder, ps + pos + 1 - is, pe, pos + 1, ie);
        
        return root;
    }
};

方法二：

class Solution {
public:
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        if (preorder.size() == 0) return NULL;
        int ppre = 0, pin = 0;
        TreeNode *root = new TreeNode(preorder.at(ppre++));
        TreeNode *p = NULL;
        stack<TreeNode *> roots;
        roots.push(root);

        while (true) {
            if (inorder.at(pin) == roots.top()->val) {
                p = roots.top();
                roots.pop();
                pin++;
                if (pin == inorder.size()) break;
                if (roots.size() && inorder.at(pin) == roots.top()->val) continue;
                p->right = new TreeNode(preorder.at(ppre));
                ppre++;
                roots.push(p->right);
            }
            else {
                p = new TreeNode(preorder.at(ppre));
                ppre++;
                roots.top()->left = p;
                roots.push(p);
            }
        }

        return root;
    }
}; 

由于vector是顺序存储的，因此没有类似于pop_front的方法，这里我们需要额外两个int变量标记当前执行到的元素位置，但整体思想是一致的。