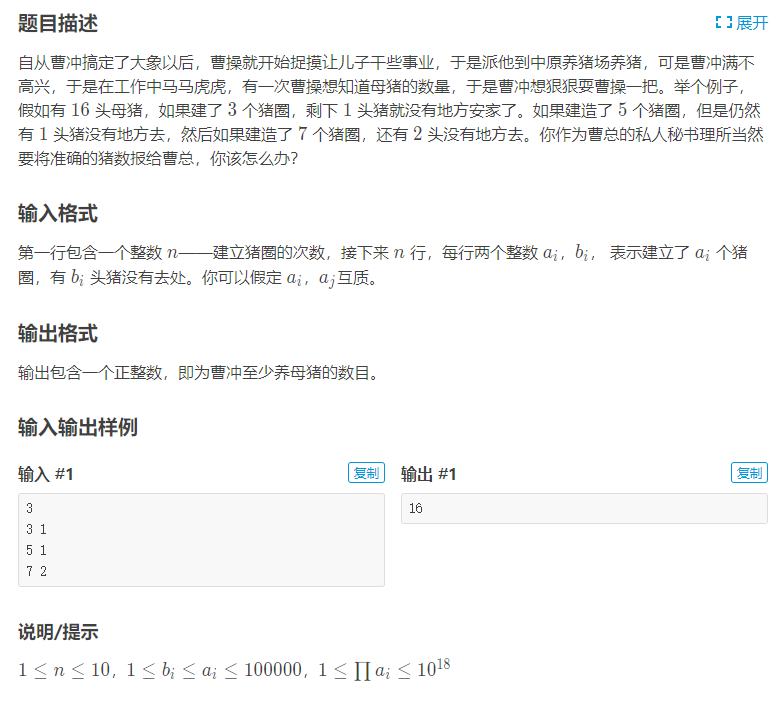
P1495 【模板】中国剩余定理(CRT)/曹冲养猪
这道题很明显是要用中国剩余定理(孙子定理)来解决。
首先,我们先看看孙子定理是怎么操作的:
我们先用一个例子来说明:
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之 剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。
具体解法分三步:
1.找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
2.用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加15∗2+21∗3+70∗2得到和233。
3.用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
那么,我们再求同余方程组的时候,就有了一个公式:
对于这样m1,m2,……,mn 两两互素,且m均为正整数的一组同余方程组
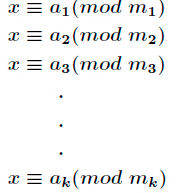
我们有这样的一个求根公式:
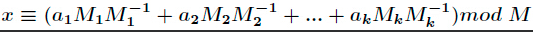
其中,ai 为最终答案除以mi 的余数,Mi 就是 M / mi 的结果 ,而M是所有的m的乘积,Mi-1 是 Mi 模 mi 的逆元
求逆元就可以使用扩展欧几里得的写法来进行求解,这样,这道问题就变得不是那么困难了
上代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<math.h> #include<cstring> using namespace std; long long n; long long a[10000],b[10000]; long long exgcd(long long a,long long b,long long &x,long long &y)//扩展欧几里得求逆元 { if(b==0) { x=1; y=0; return a; } long long g=exgcd(b,a%b,x,y);//类似于辗转相除法 long long tp=x; x=y; y=tp-a/b*y; return g; } long long crt()//中国剩余定理 { long long M=1,r=0; for(int i=1;i<=n;i++) M*=a[i];//求M for(int i=1;i<=n;i++) { long long p,y; long long m=M/a[i];//求M[i] long long d=exgcd(m,a[i],p,y);//求M[i]的逆元 ,其中 p 为我们所要求解的 x r=(r+m*b[i]*p)%M;//套用公式 } if(r<0) r+=M; return r; } int main(void) { scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i],&b[i]); printf("%lld",crt()); return 0; }