来自洛谷P1962(一道看似很水的题)
斐波那契数列的通项公式是 Fn=Fn-1 + Fn-2
在一定的复杂度内可以直接递推,但是如果n太大,那么就容易T,这时候,我们就运用矩阵加速来进行优化,以减少运行时间。
在看矩阵加速之前,我们首先需要了解矩阵快速幂
【模板】 洛谷P3390

首先,我们来讲一下矩阵与矩阵之间的运算。
1.矩阵加法:
假定有两个矩阵A,B;
一般而言,让我们进行矩阵加法的两个矩阵会是一对同型矩阵(行列数分别相等)
那么,得到的矩阵AB的第 i 行,第 j 列的元素,即为A和B中第 i 行,第 j 列的元素的加和
举个栗子:

那么减法运算就相当于加上一个负数,与之一样。
在加(减)法中,满足:
A+B=B+A【交换律】
A+(B+C)=(A+B)+C 【结合律】
2.矩阵数乘
假定我们有一个矩阵A,还有一个常数 λ,那么 λ*A 就是把A中的每一个元素都乘以 λ
再举个例子:

在矩阵的数乘中,满足如下运算规律:
设 x,y为常数
则:x(yA)= y(xA)【交换律】
(x+y)*A = xA + yA 【分配律】
(A+B)*x = xA + xB 【分配律】
3.矩阵乘法(矩阵乘矩阵)
假定我们有两个矩阵A,B。A为n*m的矩阵,B为m*k的矩阵,只有满足A的行数数等于B的列数时,才能够进行矩阵与矩阵之间的乘法运算。运算后,得到的矩阵C将会是一个n*k大小的矩阵
那么得到C矩阵的运算公式为:
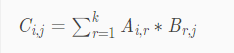
又双叒叕举个例子:
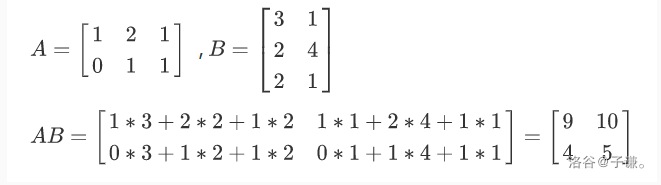
就是说,矩阵AB的第 i 行第 j 列元素都是由A的第 i 行的各个元素与B的第 j 列的各个元素相乘之和
需要注意的是,在矩阵与矩阵的乘法中,有如下运算法则
1.(AB)C=A(BC)【结合律】
2.(A+B)C=AC+BC 【分配律】
这里并没有交换律,因为将A和B的顺序颠倒后,不一定符合矩阵之间的运算定义(比如A:2*3 ; B:3*5),如果满足也不一定能够得到相同的结果。
我们在这道模板题中,因为A只是在做幂运算,并不用加入其他的递推式,我们就可以设定一个单位矩阵 L(单位矩阵的元素非0即1),使得矩阵L的第 i 行,第 i 列的元素为1,其余为0。之后可以依照快速幂的写法完成矩阵快速幂(这里用的重载运算符)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<math.h>
#include<algorithm>
using namespace std;
const long long mod=1000000007;
struct STU //声明结构体
{
long long m[110][110];
} A,I;
long long n,k;
STU operator * (const STU &a,const STU &b)//重载运算符 '*'
{
STU x;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
x.m[i][j]=0;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
for(int p=1;p<=n;p++)
{
x.m[i][j]+=a.m[i][p]*b.m[p][j]%mod; //矩阵乘法运算
x.m[i][j]%=mod;//别忘记取mod
}
}
}
return x;
}
int main(void)
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>A.m[i][j];//输入运算矩阵
}
I.m[i][i]=1;//定义单位矩阵
}
while(k>0)//快速幂运算(可以用while循环,也可以用递归)
{
if(k%2==1) I=I*A;
A=A*A;
k=k>>1;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cout<<I.m[i][j]<<" ";//输出每一个元素
}
cout<<endl;
}
return 0;
}
既然我们解决了矩阵快速幂的问题,那么再来看一下矩阵加速——【模板】洛谷 P1939(和斐波那契数列的做法差不多)。

对于这道题来说,直接递归毫无疑问是要T的,那么矩阵加速就是我们的首选算法,那么,问题来了,怎么设置我们的初始矩阵呢?
在这道题中,我们需要用第n-1个数和第n-3个数来推得第n个数
那么设现有数Fn,Fn-1,Fn-2,Fn-3
那么:Fn=Fn-1*1+Fn-2*0+Fn-3*1 ;Fn-1=Fn-1*1+Fn-2*0+Fn-3*0 ; Fn-2=Fn-1*0+Fn-2*1+Fn-3*0
则矩阵为:

那么这就是我们的初始矩阵。
值得注意的是,在这个矩阵中,第N次运算得到的结果为第N+1项,那么我们就需要输出第二行,第一列的元素即可。
上代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<math.h>
#include<cstring>
using namespace std;
const long long mod=1000000007;
struct STU //结构体
{
long long m[110][110];
} A,I;
int T,n;
STU operator * (const STU &a,const STU &b)//重载运算符
{
STU x;
for(int i=1;i<=3;i++)
{
for(int j=1;j<=3;j++)
{
x.m[i][j]=0;
}
}
for(int i=1;i<=3;i++)
{
for(int j=1;j<=3;j++)
{
for(int p=1;p<=3;p++)
{
x.m[i][j]+=a.m[i][p]*b.m[p][j]%mod;
x.m[i][j]%=mod;
}
}
}
return x;
}
void clear()
{
memset(I.m,0,sizeof(I.m));//清空I矩阵
memset(A.m,0,sizeof(A.m));//清空A矩阵
for(int i=1;i<=3;i++) I.m[i][i]=1;//还原为初始状态
A.m[1][1]=A.m[1][3]=A.m[2][1]=A.m[3][2]=1;
}
int ksm(int k)//快速幂
{
while(k>0)
{
if(k%2!=0) I=I*A;
A=A*A;
k=k>>1;
}
return I.m[2][1];
}
int ys(int k)//判断
{
if(k<=3) return 1;
else return ksm(k);
}
int main(void)
{
cin>>T;
for(int i=1;i<=T;i++)
{
cin>>n;
clear();//每一次运算后都需要清空
cout<<ys(n)<<endl;
}
return 0;
}
正题终于要来了!

看过了上面的矩阵加速例题,这道题也就变得迎刃而解。
首先,我们先定义初始矩阵,因为它只有前两项为1,那么就可以用一个1*2的矩阵L来代表,即为L【1,1】
之后,我们要定义单位矩阵,由于Fn=Fn-1+Fn-2,那么单位矩阵的第一列就应该定为:【1,1】,使得Fn-1和Fn-2能够相加
之后,为了保留下Fn-1,但Fn-2已经没有用处了,那么第二列就是【1,0】。
这样,我们的单位矩阵就是:

原式也可以化为:

到这里,我们的矩阵就构造完成了,输出时只要输出第1行第1列的元素就行了,但是,还有一个地方,那就是当我们输入N,且N大于等于3时,我们的矩阵只需要进行N-2运算,因为在本题中第1项和第二项在初始化时已经给出,进行运算时可以直接从求第三项开始。
源代码如下:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;
const long long mod=1000000007;
struct STU//结构体
{
long long m[110][110];
} A,I;
long long n;
STU operator * (const STU &a,const STU &b)//重载运算符
{
STU x;
memset(x.m,0,sizeof(x.m));
for(int i=1;i<=2;i++)
{
for(int j=1;j<=2;j++)
{
for(int k=1;k<=2;k++)
{
x.m[i][j]+=a.m[i][k]*b.m[k][j]%mod;
x.m[i][j]%=mod;
}
}
}
return x;
}
void init()//初始化
{
memset(I.m,0,sizeof(I.m));
memset(A.m,0,sizeof(A.m));
I.m[1][1]=I.m[1][2]=1;
A.m[1][1]=A.m[1][2]=A.m[2][1]=1;
}
int main(void)
{
cin>>n;
init();
if(n<=2)//第一项或第二项的情况
{
cout<<1<<endl;
return 0;
}
else //n>=3的情况
{
n=n-2;
while(n>0) //快速幂
{
if(n%2!=0) I=I*A;
A=A*A;
n=n>>1;
}
cout<<I.m[1][1]<<endl;//输出
return 0;
}
}
这样,斐波那契数列的矩阵加速解法就写完啦!
QAQ