拓扑排序

拓扑排序：

拓扑排序是根据离散数学中有关偏序与全序定义的。

 若一个集合 X 上的关系 R 是自反的 反对称的和传递的，就称为 R 是集合 X 上的 偏序关系。

设 R 是集合 X 上的偏序，若对每个 x ，y 属于 x ，必有 xRy 或 yRx，则称 R 是集合 X 上的全序关系。 

直观的讲，偏序就是一个点的集合中只有部分顶点可以确立优先关系。而全序就是点的集合中任意两个顶点都可以确立优先关系，而由某个集合上的一个偏序得到该集合的一个全序的操作就是拓扑排序。

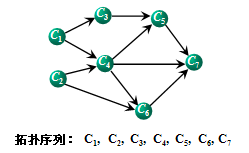
由上图可以看出，能够满足拓扑排序，首先这个图是一个有向无环图，即每一个路径都是有向的，而且其中不行成环，如果形成环就不能进行拓扑排序。

例入上图南阳理工学院课表安排：

                  课程代号                                     课程名称                                 先行课

                    C1 C2                            计算机应用基础，c语言                         无

                       C3                                               网页制作                               C1

                       C4                                        C++语言程序设计                        C1，C2

                       C5                                           数据库技术                               C3，C4

                       C6                                           汇编语言                                  C2，C4

                       C7                                          嵌入式开发                              C4，C5，C6

这就是一个类似课程先后关系的有向图，要我们根据前面的关系把这些科安排在不同的学期（即学习的先后关系）。这就要求我们对他进行一个拓扑排序。

可以看出这个排序的结果是C1,C2,C3,C4,C5,C6,C7 或者是 C2，C1，C4，C6，C3，C7。即排序后的结果不是唯一的。

那么我们怎样实现对这样一个图的拓扑排序呢，我们直到图的常用存法有两种，即临接矩阵和临接表。临接矩阵存稠密图，临接表存稀疏图，先介绍一种通过临接表存储通过DFs思想实现的算法。

从一个没有入度的节点出发，深搜回溯的时候保存最深处的点加到拓扑排序的首部。代码：

int map[Max][Max];
int vis[Max],topo[Max];
int m,n;
bool Dfs(int u)
{
    vis[u]=-1;
    for(int v=1;v<=n;v++)
    {
        if(map[u][v])
        {
            if(vis[v]<0) {return false;}
            else if(!vis[v]&&!Dfs(v)) return false;
        }
    }
    vis[u] = 1;topo[--t]=u;
    return true;
}
bool toposort()
{
    t=n;
    memset(vis,0,sizeof(vis));
    for(int u=1;u<=n;u++)
    {
        if(!vis[u]){
            if(!Dfs(u)) return false;
        }
    }
    return true;
}

裸的拓扑排序的题目：Uva10305 - Ordering Tasks

/***
*Uva10305拓扑排序
*临接矩阵存图，Dfs搜索回溯
******/
#include <stdio.h>
#include <string.h>
#define Max 120
int t;
int map[Max][Max];
int vis[Max],topo[Max];
int m,n;
bool Dfs(int u)
{
    vis[u]=-1;
    for(int v=1;v<=n;v++)
    {
        if(map[u][v])
        {
            if(vis[v]<0) {return false;}
            else if(!vis[v]&&!Dfs(v)) return false;
        }
    }
    vis[u] = 1;topo[--t]=u;
    return true;
}
bool toposort()
{
    t=n;
    memset(vis,0,sizeof(vis));
    for(int u=1;u<=n;u++)
    {
        if(!vis[u]){
            if(!Dfs(u)) return false;
        }
    }
    return true;
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==0&&m==0) break;
        memset(map,0,sizeof(map));
        for(int i=0;i<m;i++)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            map[a][b]=1;
        }
        if(toposort())
        {
            bool ok=true;
            for(int i=0;i<n;i++)
            {
                if(ok) {printf("%d",topo[i]);ok=false;}
                else printf(" %d",topo[i]);
            }
            printf("
");
        }
        else
        printf("No
");
    }
    return 0;
}