内容接自《数据结构基础知识(1)》。。。
链表的分类
单链表
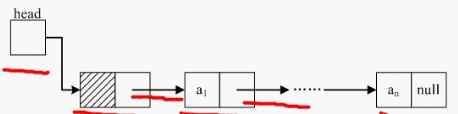
单链表是一种链式存取的结构,为找第 i 个数据元素,必须先找到第 i-1 个数据元素。图中阴影区域表示数据域,空白区表示指针域。而且最后一个指针域为空。
循环链表
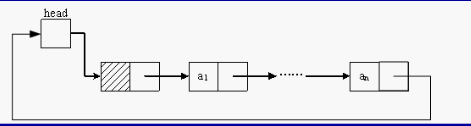
循环链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点,整个链表形成一个环。循环链表又分为单循环链表和多重链的循环链表。
双链表
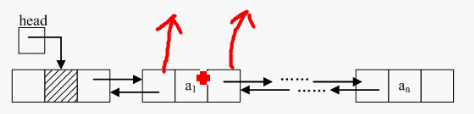
双链表也称为双向链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。双链表的灵活度要比单链表好一些,但开支要大一些(存在两个指针)。
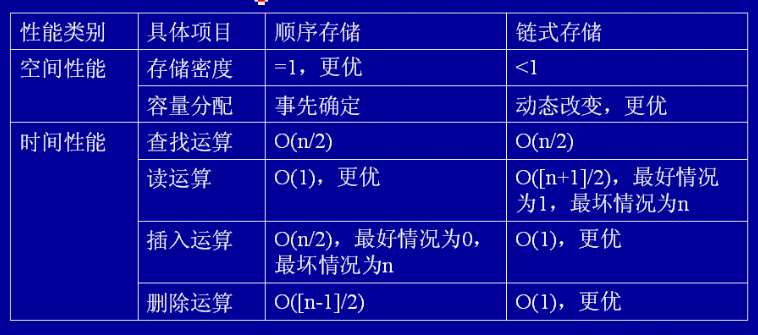
顺序表与链表的比较
顺序表存储位置是相邻连续的,可以随即访问的一种数据结构,一个顺序表在使用前必须指定起长度,一旦分配内存,则在使用中不可以动态的更改。他的优点是访问数据是比较方便,可以随即的访问表中的任何一个数据。
链表是通过指针来描述元素关系的一种数据结构,他可以是物理地址不连续的物理空间。不能随即访问链表元素,必须从表头开始,一步一步搜索元素。它的优点是:对于数组,可以动态的改变数据的长度,分配物理空间。
在使用中:如果一个数组在使用中,查询比较多,而插入,删除数据比较少,数组的长度不变时,选顺序表比较合理。如果插入,删除,长度不定的数组,可以选链表。
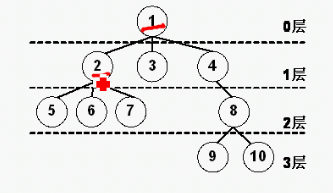
树(Tree)
树是包含n(n>0)个结点的有穷集合K,且在K中定义了一个关系N,N满足 以下条件:
(1)有且仅有一个结点 K0,他对于关系N来说没有前驱,称K0为树的根结点。简称为根(root)。
(2)除K0外,K中的每个结点,对于关系N来说有且仅有一个前驱。
(3)K中各结点,对关系N来说可以有m个后继(m>=0)。
树具有以下特点:
(1) 每个节点有零个或多个子节点。
(2) 每个子节点只有一个父节点。
(3) 没有父节点的节点称为根节点。
关于树的一些术语
节点的度:一个节点含有的子树的个数称为该节点的度;
叶节点或终端节点:度为零的节点称为叶节点;
非终端节点或分支节点:度不为零的节点;
双亲节点或父节点:若一个结点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的高度或深度:定义一棵树的根结点层次为1,其他节点的层次是其父结点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。节点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的度:一棵树中,最大的节点的度称为树的度;
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的遍历
树的遍历分为:前序遍历、后序遍历、层次遍历。前序遍历的遍历顺序是先访问根结点,再访问叶子结点;后序遍历的遍历顺序是先访问叶子结点,再访问根结点;而层次遍历则是按层次进行遍历。

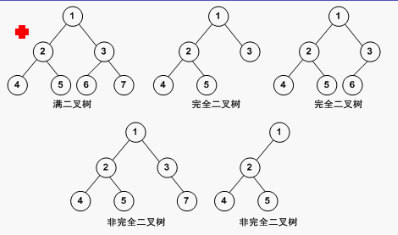
二叉树
二叉树是每个节点最多有两个子树的有序树。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树又分为满二叉树、完全二叉树、非完全二叉树等。
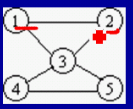
图(Graph)
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对,若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。其中,图分为无向图和有向图。
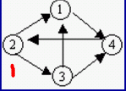
图的遍历
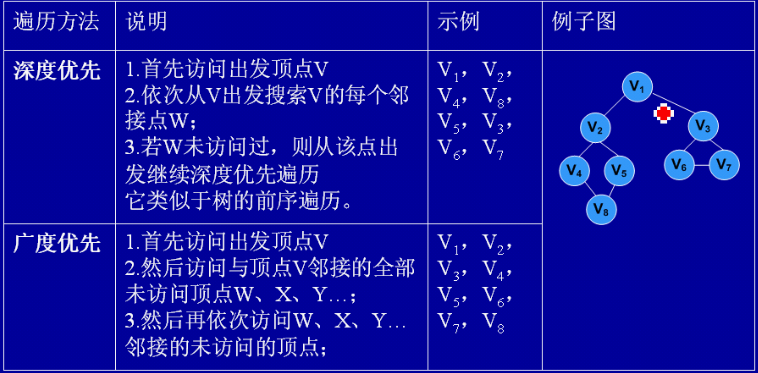
图的遍历分为深度优先遍历和广度优先遍历。深度优先遍历的思想类似于树的先序遍历。其遍历过程可以描述为:从图中某个顶点v出发,访问该顶点,然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点,直至图中所有与v有路径相通的顶点都被访问完为止。
广度优先遍历方法描述为:从图中某个顶点v出发,在访问该顶点v之后,依次访问v的所有未被访问过的邻接点,然后再访问每个邻接点的邻接点,且访问顺序应保持先被访问的顶点其邻接点也优先被访问,直到图中的所有顶点都被访问为止。