在项目中有时会使用到比较精确的计算,比如涉及到钱的计算,这个时候不会采用float或者double类型来进行。需要使用bigdeciml类型来进行大数的精确运算。
一、BigDecimal的基本运算——加减乘除绝对值
BigDecimal初始化时尽量全部使用string的构造函数,不然的话可能有出现错误
BigDecimal num1 = new BigDecimal("2");
BigDecimal num2 = new BigDecimal("3");
我们对其进行加、减、乘、除、绝对值的运算其实质就是对Bigdecimal的类的一些方法调用:加法 add()函数、减法subtract()函数、乘法multiply()函数、除法divide()函数、绝对值abs()函数。
//加法
BigDecimal result1 = num1.add(num2);
//减法
BigDecimal result2 = num1.subtract(num2);
//乘法
BigDecimal result3 = num1.multiply(num2);
//除法
BigDecimal result5 = num2.divide(num1,2,BigDecimal.ROUND_HALF_UP);
//绝对值
BigDecimal result4 = num3.abs();
需要注意的是:
(1)System.out.println()中的数字默认是double类型的,double类型小数计算不精准。
(2)使用BigDecimal类构造方法传入double类型时,计算的结果也是不精确的。
因为不是所有的浮点数都能够被精确的表示成一个double 类型值,因此它会被表示成与它最接近的double 类型的值。所以在需要精确计算时必须改用传入String的构造方法,这样才能得到更加精确的计算结果。
二、除法divide()参数使用
使用除法函数在divide的时候要设置各种参数,要精确的小数位数和舍入模式,不然会出现报错。
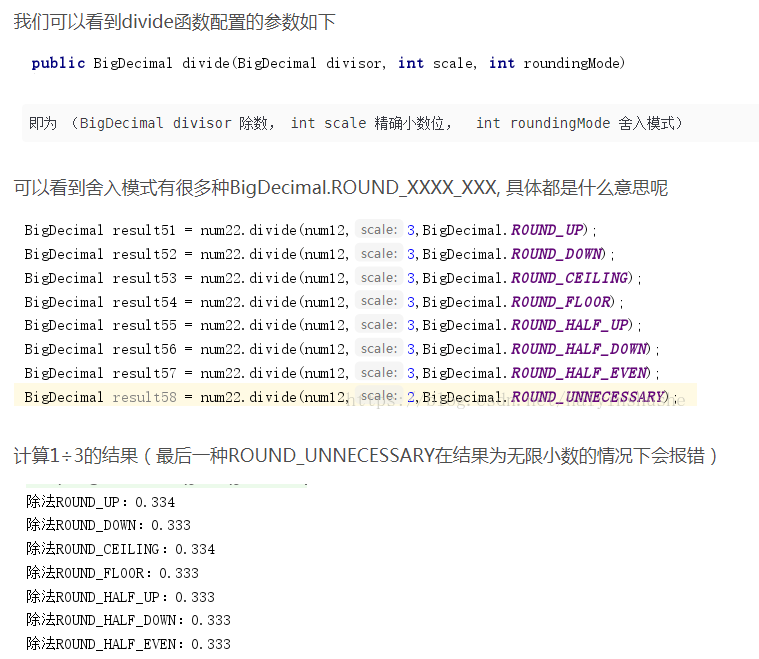
对这八种舍入模式解释如下
1、ROUND_UP:舍入远离零的舍入模式,在丢弃非零部分之前始终增加数字(始终对非零舍弃部分前面的数字加1),注意,此舍入模式始终不会减少计算值的大小。
2、ROUND_DOWN:接近零的舍入模式。在丢弃某部分之前始终不增加数字(从不对舍弃部分前面的数字加1,即截短)。注意,此舍入模式始终不会增加计算值的大小。
3、ROUND_CEILING:接近正无穷大的舍入模式。如果 BigDecimal 为正,则舍入行为与 ROUND_UP 相同;如果为负,则舍入行为与 ROUND_DOWN 相同。
注意,此舍入模式始终不会减少计算值。
4、ROUND_FLOOR:接近负无穷大的舍入模式。如果 BigDecimal 为正,则舍入行为与 ROUND_DOWN 相同;如果为负,则舍入行为与 ROUND_UP 相同。
注意,此舍入模式始终不会增加计算值。
5、ROUND_HALF_UP:向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则为向上舍入的舍入模式。如果舍弃部分 >= 0.5,则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同。注意,这是我们大多数人在小学时就学过的舍入模式(四舍五入)。
6、ROUND_HALF_DOWN:向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则为上舍入的舍入模式。如果舍弃部分 > 0.5,则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同(五舍六入)。
7、ROUND_HALF_EVEN:向“最接近的”数字舍入,如果与两个相邻数字的距离相等,则向相邻的偶数舍入。如果舍弃部分左边的数字为奇数,则舍入行为与 ROUND_HALF_UP 相同;如果为偶数,则舍入行为与 ROUND_HALF_DOWN 相同。注意,在重复进行一系列计算时,此舍入模式可以将累加错误减到最小。
此舍入模式也称为“银行家舍入法”,主要在美国使用。四舍六入,五分两种情况。如果前一位为奇数,则入位,否则舍去。
以下例子为保留小数点1位,那么这种舍入方式下的结果。1.15>1.2 1.25>1.2
8、ROUND_UNNECESSARY:断言请求的操作具有精确的结果,因此不需要舍入。如果对获得精确结果的操作指定此舍入模式,则抛出ArithmeticException。
参考博文:
(1) https://blog.csdn.net/haiyinshushe/article/details/82721234