下载附件后,打开来为四个签名文件、被签名的信息以及一份pem形式的公钥
题目提示说此题的攻击方式曾被用于PS3的破解。
首先了解一下DSA的签名以及验证的过程。
在签名和验证之前,需要确定过程所需要的参数。
公钥密钥:(公钥)
P:512~1024位的素数
Q:160位长,并于p-1互素的因子
G:(g=h^{(p-1)/q} mod p),其中 h 小于 p-1 并且 (h^{(p-1)/q} mod p > 1)
Y:(g^{x} mod p)(此处的x为私钥)
私钥:
x:x<q
签名过程:
①随机选取<q的一个随机数k
②算出(r=(g^k mod p)mod q)
③算出(s=k^{-1}*(H(m)+r*s) mod q),此处的h(m)为对消息m进行哈希运算
④得出签名为(r,s)
验证过程:
①算出(w=s^{-1} mod q)
②算出(u1=H(m)*w mod q)
③算出(u2=r*w mod q)
④算出v=((g^{u1})*(y^{u2}) mod q)
⑤若v==r,则签名有效,验证成功
了解DSA签名与验证的过程后,再了解对于破解PS3的攻击方式。这种方式其实就是基于随机数k的重用攻击。
如果在对消息的签名过程中,k的取值相同,那么得出的签名r是相同的,假设有两份签名,(r1,s1)与(r2,s2)且随机值k相等,则:
r1=r2
(s1=(k^{-1})*(H(m1)+r1*x) mod q) —①
(s2=(k^{-1})*(H(m2)+r2*x) mod q) —②
利用②-①则
((s2-s1)=(k^{-1})*(H(m2)-H(m1)) mod q)
再转换一下得:
(k=((s2-s1)^{-1}) *(H(m2)-H(m1)) mod q)
得到k后,就可以根据①式或者②式得到私钥x,这里利用①式
(x=(s1*k-H(m1))*(r1^{-1}) mod q)
了解完原理后,转到题目中来,如果运用了PS3的破解攻击方式,那么签名中的r一定是相等的,使用010editor 观察每份签名文件,发现sign3.bin与sign4.bin的前部分字节相等。

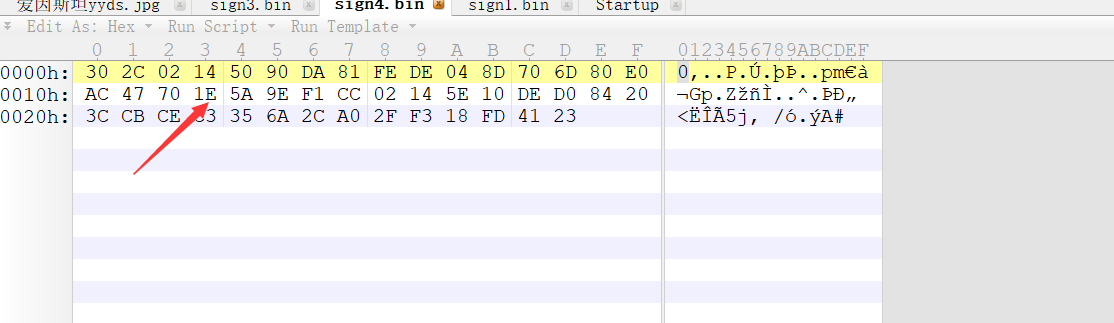
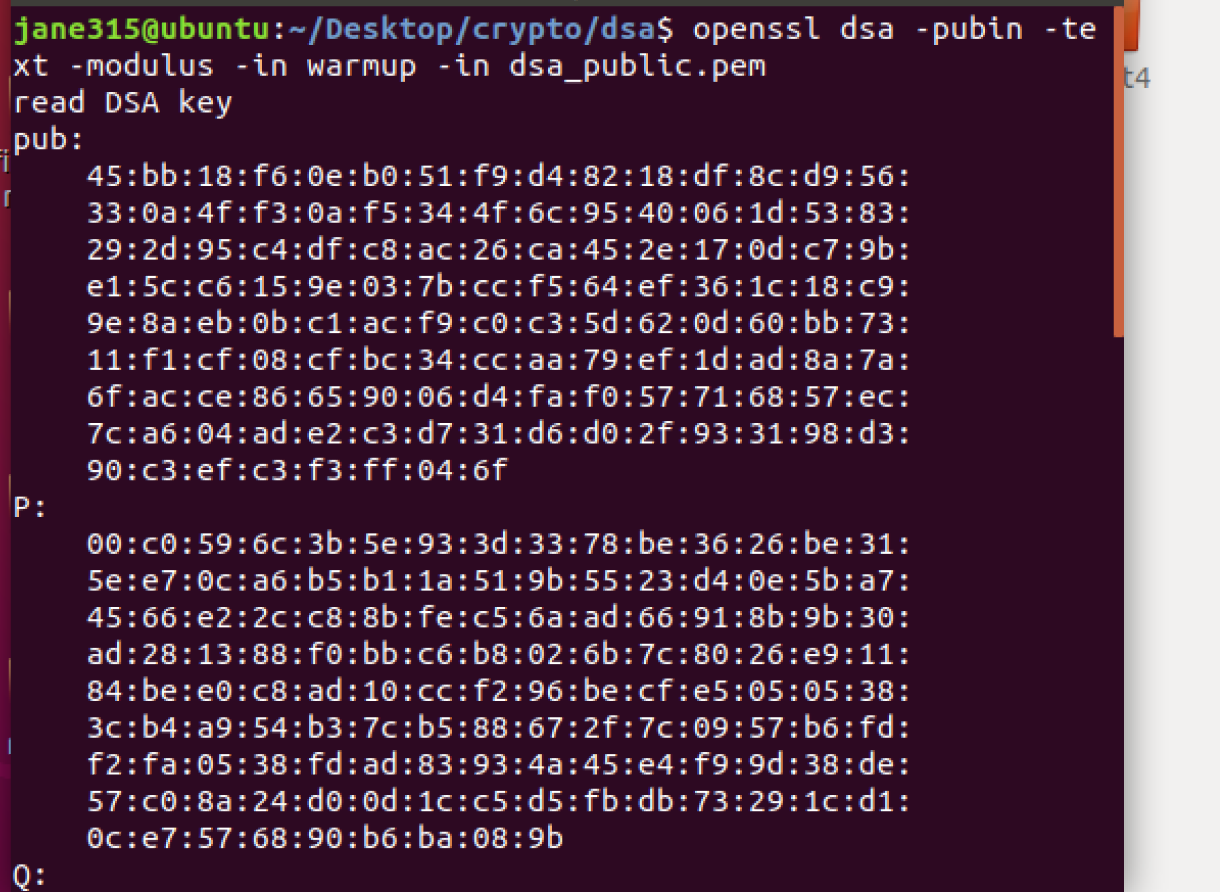
这里需要注意的是已知q的位数为160位,因此r和s的位数都小于160位,观察这两份文件的sign.bin的字节,发现前26个字节都相等,说明需要判断r与s的具体位置,可以观察得出0x0214很特殊,0x0124往后到下一个0x0214之前便是r,下一个0x0214之后便是s。最后,再根据pem文件格式的公钥,使用openssl来得到其中的p、q、g、y
这里简介一下这里的用法
-in val Input key(val是个参数变量;如,-in key 就是放入密钥)
-text Print the key in text (打印公钥的参数值)
-modulus Print the DSA public value(打印出pub的值)
-pubin Expect a public key in input file(放入需要解析公钥的输入文件)
from Crypto.Util.number import *
from libnum import *
import hashlib
from Crypto.Hash import SHA
y=0x45BB18F60EB051F9D48218DF8CD956330A4FF30AF5344F6C9540061D5383292D95C4DFC8AC26CA452E170DC79BE15CC6159E037BCCF564EF361C18C99E8AEB0BC1ACF9C0C35D620D60BB7311F1CF08CFBC34CCAA79EF1DAD8A7A6FACCE86659006D4FAF057716857EC7CA604ADE2C3D731D6D02F933198D390C3EFC3F3FF046F
p=0xc0596c3b5e933d3378be3626be315ee70ca6b5b11a519b5523d40e5ba74566e22cc88bfec56aad66918b9b30ad281388f0bbc6b8026b7c8026e91184bee0c8ad10ccf296becfe50505383cb4a954b37cb588672f7c0957b6fdf2fa0538fdad83934a45e4f99d38de57c08a24d00d1cc5d5fbdb73291cd10ce7576890b6ba089b
q=0x868f78b8c8500bebf67a58e33c1f539d3570d1bd
g=0x4cd5e6b66a6eb7e92794e3611f4153cb11af5a08d9d4f8a3f250037291ba5fff3c29a8c37bc4ee5f98ec17f418bc7161016c94c84902e4003a7987f0d8cf6a61c13afd5673caa5fb411508cdb3501bdff73e747925f76586f4079fea12098b3450844a2a9e5d0a99bd865e0570d5197df4a1c9b8018fb99cdce9157b98500179
r1=0x5090DA81FEDE048D706D80E0AC47701E5A9EF1CC
s2=0x5E10DED084203CCBCEC3356A2CA02FF318FD4123
s1=0x30EB88E6A4BFB1B16728A974210AE4E41B42677D
m1=open("C:ctf_exercisejarvisdsadsapacket3message3","rb")
m1=(m1.read())
m2=open("C:ctf_exercisejarvisdsadsapacket4message4","rb")
m2=(m2.read())
sha = SHA.new()
sha.update(m1)
hm1=int(sha.hexdigest(),16)
sha = SHA.new()
sha.update(m2)
hm2=int(sha.hexdigest(),16)
print(hm1,hm2)
k=((hm2-hm1)*invmod((s2-s1),q))%q
x=(s1k-hm1)invmod(r1,q)
print(x%q)
运行结果如下:

得到flag:CTF{520793588153805320783422521615148687785086070744}