第三届江西省网络安全大赛-部分Crypto

一、Round

题目附件如下：

 比赛题目flag为'CMISCCTF{}'的模式，可以发现':D@J::K=r<ecXi^[V:XjXit'字符串中，'字符:'的位置恰对应于flag格式中'C'的位置，猜测为移位密码，脚本如下：

c=':D@J::K=r<ecXi^[V:XjXit'

x=ord(':')-ord('C')
flag=''
for i in c:
    temp=chr((ord(i)-x)%126)
    flag+=temp

print(flag)

运行结果如下：

 二、Factor

附件内容如下：

n = 3454083680130687060405946528826790951695785465926614724373
e = 3
c = 1347530713288996422676156069761604101177635382955634367208
gcd(m, n) = 1

明显的RSA,将n分解得三个因数：

p=11761833764528579549

q=17100682436035561357

r=17172929050033177661

下面求n得欧拉函数，当直接phi=(p-1)*(q-1)*(r-1)时，发现e和phi有公约数，求不出私钥d,使用gcd发现，e和p有最大公约数3，因此得稍微推下式子。

因为e和(q-1)和(r-1)是互质的，故可推出

 写出脚本如下：

from libnum import *
def gcd(a, b):
   if a < b:
     a, b = b, a
   while b != 0:
     temp = a % b
     a = b
     b = temp
   return a

n = 3454083680130687060405946528826790951695785465926614724373
c = 1347530713288996422676156069761604101177635382955634367208
p= 17100682436035561357
q= 11761833764528579549
r= 17172929050033177661
e=3
print(gcd(p-1,e),gcd(q-1,e),gcd(r-1,e))
inve_qr=invmod(e,(q-1)*(r-1))
invd=(e*inve_qr,(q-1)*(r-1))
m=pow(c,inve_qr,q*r)
print(n2s(m))

运行结果如下：

 三、Change

给出了两个文件，change.py如下：

from flag import FLAG
from Crypto.Util.number import *
import gmpy2
import random

while True:
    p = int(gmpy2.next_prime(random.randint(10**399, 10**400-1)))
    q = int(str(p)[200:]+str(p)[:200])
    if gmpy2.is_prime(q):
        break

m = bytes_to_long(FLAG)
n = p*q
e = 65537
c = pow(m,e,n)

with open("enc","wb") as f:
    f.write(str(c))
    f.write("
")
    f.write(str(n))

#182812482972168423884795132699225934365072979206288632257180603530046820174392675977209758378734399146216742345585898385168866887000708558119959898992294085847474548306743585711154035585848291290988967352517174312220756638881837930962458861193652684492265539096477345065113556380573776423787885892688197584678128636231428194711357642971544417113415626331810909274966752557628893585198569815939514862013512237657828262360291726912615575646318630641527418369988268899879152029186728850816178597399494254385226049249357897840618728804680238123954207656671747782543031545429711152272581734051959578453680011676521727918037340906791388178004979453256050227967701258768070039292546964652071924183467364467145178290753361477912582242961929982420950384199259355122986865808523351306098081481072454093823090
#438980397031315392229453908048509540832246041631432878509579665664182747463100230160823865621798053164989325086085003940181731721089701380743698761443812523024144817205902380903062054138730658451286904347536210833160924917347633148983052015550354913154312162901555870494273903714349869746793861874257201085777893961715468950661641778512110325457371446203379767458862059193946434683324578530163650541637261158037041205642428802942295011562277084687025213626698849526240663754073508102229066475773893638716845176469070938803298515155140240970836387785401085919369741520890271902332951669953411373633688944162470994856654604872287103746922041844065053274059990595496159866206551119361036237431289830985174384522423364811997241255005514248198447925396378192915553898993758660041223393168707380580012437

enc文件如下：

182812482972168423884795132699225934365072979206288632257180603530046820174392675977209758378734399146216742345585898385168866887000708558119959898992294085847474548306743585711154035585848291290988967352517174312220756638881837930962458861193652684492265539096477345065113556380573776423787885892688197584678128636231428194711357642971544417113415626331810909274966752557628893585198569815939514862013512237657828262360291726912615575646318630641527418369988268899879152029186728850816178597399494254385226049249357897840618728804680238123954207656671747782543031545429711152272581734051959578453680011676521727918037340906791388178004979453256050227967701258768070039292546964652071924183467364467145178290753361477912582242961929982420950384199259355122986865808523351306098081481072454093823090
438980397031315392229453908048509540832246041631432878509579665664182747463100230160823865621798053164989325086085003940181731721089701380743698761443812523024144817205902380903062054138730658451286904347536210833160924917347633148983052015550354913154312162901555870494273903714349869746793861874257201085777893961715468950661641778512110325457371446203379767458862059193946434683324578530163650541637261158037041205642428802942295011562277084687025213626698849526240663754073508102229066475773893638716845176469070938803298515155140240970836387785401085919369741520890271902332951669953411373633688944162470994856654604872287103746922041844065053274059990595496159866206551119361036237431289830985174384522423364811997241255005514248198447925396378192915553898993758660041223393168707380580012437

明显这也是一个RSA的题，但有点点不同，p=一个在[10**399, 10**400-1]的大素数，而q=int(str(p)[200:]+str(p)[:200]),与p的值息息相关，就是把高200位和低200位互换了，因此我们可以假设p=A*(10^200)+B，而q=B*(10^200)+A,如下：

n=(A*B)*(10^400)+(A*A+B*B)*(10^200)+A*B

而n的取值可以画为以下四段：

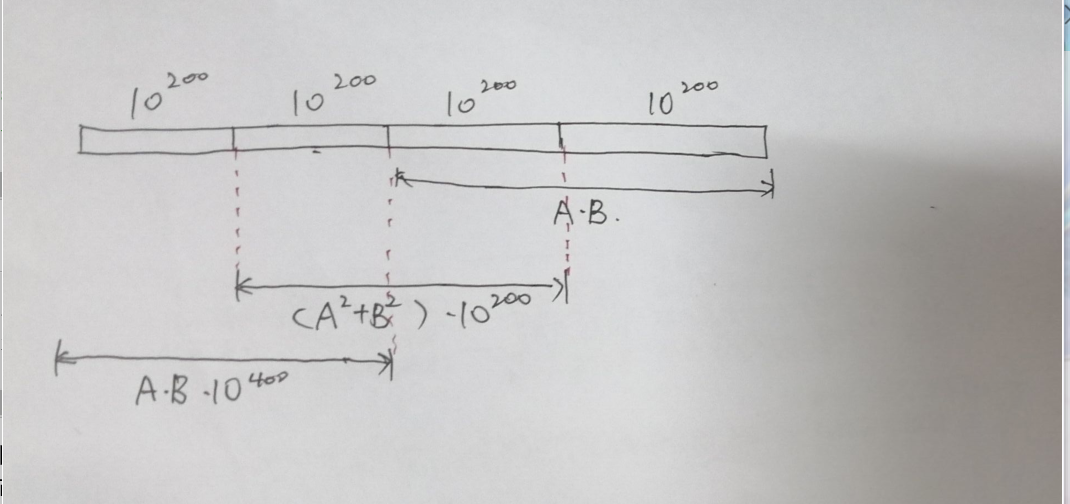
 要注意的就是中间一段(A*A+B*B)*(10^200)可能回向高200位进位，因此我们可以得到以下四个式子：(顺序从左往右)

n1=n//(10^600)

n2=(n//(10^400))%(10^200)

n3=(n//(10^200))%(10^200)

n4=n%(10^200)

故若(A*A+B*B)*(10^200)进位，则A*B=(n1-1)*(10^200)+n4,若不进位，则等于A*B=(n1)*(10^200)+n4

因此，可以把A*B求出来，再把(A*A+B*B)的值求出，即可根据这两者解出A和B的值

写出脚本如下：

import gmpy2
from libnum import invmod,n2s

c=182812482972168423884795132699225934365072979206288632257180603530046820174392675977209758378734399146216742345585898385168866887000708558119959898992294085847474548306743585711154035585848291290988967352517174312220756638881837930962458861193652684492265539096477345065113556380573776423787885892688197584678128636231428194711357642971544417113415626331810909274966752557628893585198569815939514862013512237657828262360291726912615575646318630641527418369988268899879152029186728850816178597399494254385226049249357897840618728804680238123954207656671747782543031545429711152272581734051959578453680011676521727918037340906791388178004979453256050227967701258768070039292546964652071924183467364467145178290753361477912582242961929982420950384199259355122986865808523351306098081481072454093823090
n=438980397031315392229453908048509540832246041631432878509579665664182747463100230160823865621798053164989325086085003940181731721089701380743698761443812523024144817205902380903062054138730658451286904347536210833160924917347633148983052015550354913154312162901555870494273903714349869746793861874257201085777893961715468950661641778512110325457371446203379767458862059193946434683324578530163650541637261158037041205642428802942295011562277084687025213626698849526240663754073508102229066475773893638716845176469070938803298515155140240970836387785401085919369741520890271902332951669953411373633688944162470994856654604872287103746922041844065053274059990595496159866206551119361036237431289830985174384522423364811997241255005514248198447925396378192915553898993758660041223393168707380580012437

e=65537 
n1=n//(10**600) 
n2=(n//(10**400))%(10**200) 
n3=(n//(10**200))%(10**200) 
n4=n%(10**200) 
AB=0 
if ((n2//10**199)>=n4//(10**199)):#未进位情况 
　　AB=n1*(10**200)+n4 
else:#进位情况 
　　AB=(n1-1)*(10**200)+n4 
A2B2=(n-AB*(10**400+1))//(10**200)#A*A+B*B 
AaddB=int(gmpy2.iroot(A2B2+2*AB,2)[0])#A+B 
A_B=int(gmpy2.iroot((A2B2-2*AB),2)[0])#A-B 
A=(AaddB+A_B)//2 
B=(AaddB-A_B)//2 
p=A*(10**200)+B 
q=B*(10**200)+A 
phi=(p-1)*(q-1) 
invd=invmod(e,phi)
m=pow(c,invd,n) 
print(n2s(m))

运行即可得出结果！