【快速排序】:
利用递归算法, 首先选择一个基准值(pivot value),这里我们选列表的第一个值作为例。这个基准值的作用是协助列表的分割。
这个基准值在正序列表中的正确位置,我们称之为分割点(split point)。这个点用于将列表分成两个部分,然后再对每个部分做快速排序。
分割过程如下:
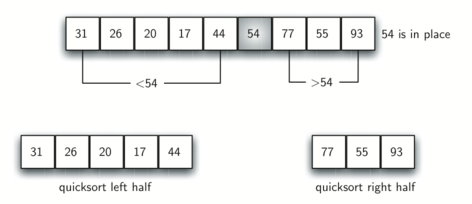
首先我们选择列表首个元素作为基准值,这个例子中即为54

接下来寻找分割点,在这个过程中同时会将小于基准值的元素移动到分割点左边,将大于基准值的元素移动到分割点右边。
为了完成上述操作,我们设置两个标记符leftmark和rightmark来追踪扫描各个元素的过程:
当leftmark位置的元素小于或等于基准值时,leftmark向右移动一个位置继续扫描;当leftmark位置的元素大于基准值时停止扫描。
同理,当rightmark位置的元素大于或等于基准值时,rightmark向左移动一个位置继续扫描;当rightmark位置的元素小于基准值时停止扫描。
停止扫描后,我们比较leftmark和rightmark的大小,如果rightmark<leftmark,rightmark就是基准值应该存放的位置,也就是分割点,我们将基准值交换到这个位置,返回分割点位置以便下一步递归操作;否则交换两个位置的元素。

将基准值存放到正确的位置后,我们看到现在的列表中,在基准值左侧的元素都小于基准值,在右侧的元素都大于基准值。所以我们以基准值为分割点,将列表分成左右两个子列表,再继续对子列表做快速排序,直到子列表的长度为0或1。
【 implementation of quick sort 】

【 performance analysis】
和归并排序相比,快速排序不需要多余的空间;但缺点是列表有可能不是平均分割的,将导致效率降低。
最坏的情况就是每次分割都是将列表分成一个长度为0的子列表和一个长度为n-1的子列表, 这种情况下,时间复杂度为O(n2)。
我们可以通过改变基准值的选取方法来减弱这种不平均分割的现象,一种方法是选取列表第一个元素,中间元素,最后一个元素中数值大小处于中间的那个值作为基准值。