Trees Made to Order
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6290 | Accepted: 3619 |
Description
We can number binary trees using the following scheme:
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.
The first 10 binary trees and tree number 20 in this sequence are shown below:
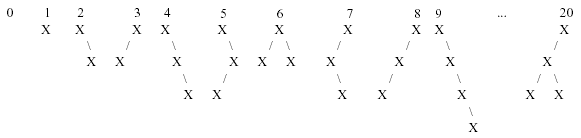
Your job for this problem is to output a binary tree when given its order number.
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.
The first 10 binary trees and tree number 20 in this sequence are shown below:
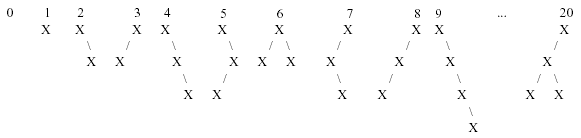
Your job for this problem is to output a binary tree when given its order number.
Input
Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)
Output
For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:
A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.
A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.
Sample Input
1 20 31117532 0
Sample Output
X ((X)X(X))X (X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)
Source
卡特兰数学习: http://www.cnblogs.com/jackge/archive/2013/05/19/3086519.html
预处理卡特兰数之后,可以推出当前是多少个节点组成的二叉树,也知道是在当前节点所有排序中的名次
然后开始递归,从右子树开始枚举,判断左右子树的节点个数,递归。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; long long C[30]={1}; void Init(){ //预处理卡特兰数 for(int i=1;i<=25;i++) C[i]=C[i-1]*(4*i-2)/(i+1); } void solve(int k,int cnt){ //输出k个节点的并排在第cnt位的二叉树 if(k==1){ //只有一个节点,直接输出 printf("X"); return ; } if(cnt<=C[k-1]){ //排名很靠前,只有右子树 printf("X"); printf("("); solve(k-1,cnt); printf(")"); }else if(cnt>C[k]-C[k-1]){ //排名很靠后,只有左子树 printf("("); solve(k-1,cnt-(C[k]-C[k-1])); printf(")"); printf("X"); }else{ int t=k-1,m; for(int i=t;i>=0;i--){ //判断左右子树各有多少个节点,更新名次 if(C[i]*C[t-i]<cnt) cnt-=C[i]*C[t-i]; else{ m=i; break; } } printf("("); solve(t-m,cnt/C[m]+(cnt%C[m]!=0)); //递归左子树 printf(")X("); solve(m,(cnt-1)%C[m]+1); //递归右子树 printf(")"); } } int main(){ //freopen("input.txt","r",stdin); int n,m; Init(); while(~scanf("%d",&n) && n){ for(int i=1;;i++){ if(n>C[i]) n-=C[i]; else{ m=i; break; } } solve(m,n); printf("\n"); } return 0; }