Tobo or not Tobo
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 9 Accepted Submission(s) : 6
Problem Description
The game of Tobo is played on a plastic board designed into a 3 × 3 grid with cells numbered from 1 to 9 as shown in figure (a). The grid has four dials (labeled ``A" to ``D" in the figure.) Each dial can be rotated in 90 degrees increment in either direction. Rotating a dial causes the four cells currently adjacent to it to rotate along. For example, figure (b) shows the Tobo after rotating dial ``A" once in a clockwise direction. Figure (c) shows the Tobo in figure (b) after rotating dial ``D" once in a counterclockwise direction. 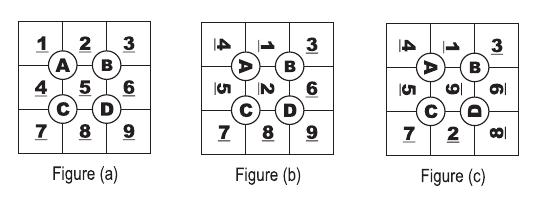

Input
Your program will be tested on one or more test cases. Each test case is specified on a line by itself. Each line is made of 10 decimal digits. Let's call the first digit Y . The remaining 9 digits are non-zeros and describe the current arrangement of the Tobo in a row-major top-down, left-to-right ordering. The first sample case corresponds to figure (c).
The last line of the input file is a sequence of 10 zeros.
The last line of the input file is a sequence of 10 zeros.
Output
For each test case, print the result using the following format:
k . R
where k is the test case number (starting at 1,) is a single space, and R is the minimum number of rotations needed to bring the Tobo back to its standard arrangement. If this can't be done in Y dials or less, then R = -1.
k . R
where k is the test case number (starting at 1,) is a single space, and R is the minimum number of rotations needed to bring the Tobo back to its standard arrangement. If this can't be done in Y dials or less, then R = -1.
Sample Input
3413569728 1165432789 0000000000
Sample Output
1. 2 2. -1
Source
2008 ANARC
继续IDA*搜索,估价函数H仍然是曼哈顿距离,每一次转换会改变4个位置的曼哈顿距离,分别改变1,所以把曼哈顿距离和+3/4便可以作为H函数,表示至少需要多少步,一个DFS的剪枝。
这题最多九步,BFS应该也无压力
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int a[9]; int depth,flag; char str[10]; int rotation[4][4]={{0,1,4,3},{1,2,5,4},{3,4,7,6},{4,5,8,7}}; int abs(int x){ return x<0?-x:x; } int H(int *b){ int ans=0; for(int i=0;i<9;i++) ans+=abs(i/3-(b[i]-1)/3)+abs(i%3-(b[i]-1)%3); return (ans+3)/4; } void change(int *b,int k){ if(k&1){ //顺时针旋转 k>>=1; int tmp=b[rotation[k][3]]; for(int i=3;i>0;i--) b[rotation[k][i]]=b[rotation[k][i-1]]; b[rotation[k][0]]=tmp; }else{ //逆时针旋转 k>>=1; int tmp=b[rotation[k][0]]; for(int i=1;i<4;i++) b[rotation[k][i-1]]=b[rotation[k][i]]; b[rotation[k][3]]=tmp; } } void IDAstar(int *b,int curDepth,int dir){ if(flag) return ; if(H(b)>curDepth) return ; if(curDepth==0 && H(b)==0){ flag=1; return ; } for(int i=0;i<8;i++){ if(dir!=-1 && dir/2==i/2 && (dir%2)^(i%2)) continue; int tmp[9]; for(int j=0;j<9;j++) tmp[j]=b[j]; change(tmp,i); IDAstar(tmp,curDepth-1,i); } } int main(){ //freopen("input.txt","r",stdin); int cases=0; while(~scanf("%s",str) && strcmp(str,"0000000000")){ int t=str[0]-'0'; for(int i=0;i<9;i++) a[i]=str[i+1]-'0'; flag=0; for(depth=H(a);depth<=t;depth++){ IDAstar(a,depth,-1); if(flag){ printf("%d. %d\n",++cases,depth); break; } } if(!flag) printf("%d. -1\n",++cases); } return 0; }