A Famous Grid
Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 798 Accepted Submission(s): 318
Problem Description
Mr. B has recently discovered the grid named "spiral grid".
Construct the grid like the following figure. (The grid is actually infinite. The figure is only a small part of it.)
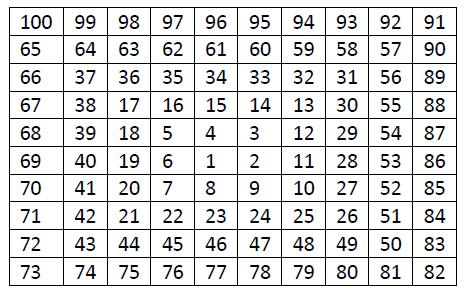
Considering traveling in it, you are free to any cell containing a composite number or 1, but traveling to any cell containing a prime number is disallowed. You can travel up, down, left or right, but not diagonally. Write a program to find the length of the shortest path between pairs of nonprime numbers, or report it's impossible.
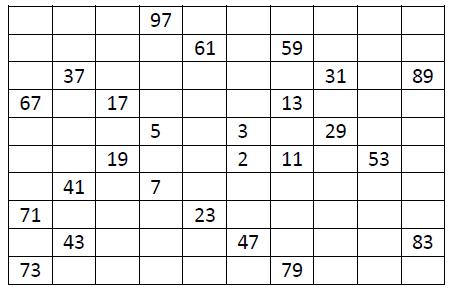
Construct the grid like the following figure. (The grid is actually infinite. The figure is only a small part of it.)

Considering traveling in it, you are free to any cell containing a composite number or 1, but traveling to any cell containing a prime number is disallowed. You can travel up, down, left or right, but not diagonally. Write a program to find the length of the shortest path between pairs of nonprime numbers, or report it's impossible.

Input
Each test case is described by a line of input containing two nonprime integer 1 <=x, y<=10,000.
Output
For each test case, display its case number followed by the length of the shortest path or "impossible" (without quotes) in one line.
Sample Input
1 4
9 32
10 12
Sample Output
Case 1: 1
Case 2: 7
Case 3: impossible
Source
题目大意:有螺旋数组成的图,素数不能过,求两个数之间怎么过最短。
这个x,y《=10000,模拟图的时候最好按40000建图
1 #include<iostream> 2 #include<queue> 3 #include<cstdio> 4 #include<cstring> 5 6 using namespace std; 7 8 int X,Y; 9 int map[210][210],vis[210][210]; 10 int prime[40010]; 11 12 void getPrime(){ 13 memset(prime,1,sizeof(prime)); 14 prime[1]=0; 15 for(int i=2;i<40010;i++) 16 if(prime[i]) 17 for(int j=i*i;j<40010;j+=i) 18 prime[j]=0; 19 } 20 21 void Graph(){ 22 int c=40000; 23 int i,x=1,y=200,a=1,b=200; 24 while(c>0){ 25 for(i=x;i<=y;i++) 26 map[x][i]=c--; 27 x++; 28 for(i=x;i<=y;i++) 29 map[i][y]=c--; 30 y--; 31 for(i=y;i>=a;i--) 32 map[b][i]=c--; 33 b--; 34 for(i=b;i>a;i--) 35 map[i][a]=c--; 36 a++; 37 } 38 } 39 40 struct node{ 41 int x,y; 42 int step; 43 }; 44 45 int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; 46 47 int BFS(int si,int sj,int c){ 48 queue<node> q; 49 while(!q.empty()) 50 q.pop(); 51 node info,tmp; 52 memset(vis,0,sizeof(vis)); 53 info.x=si,info.y=sj,info.step=c; 54 vis[si][sj]=1; 55 if(map[info.x][info.y]==Y) 56 return info.step; 57 q.push(info); 58 while(!q.empty()){ 59 tmp=q.front(); 60 q.pop(); 61 for(int i=0;i<4;i++){ 62 info.x=tmp.x+dir[i][0]; 63 info.y=tmp.y+dir[i][1]; 64 info.step=tmp.step+1; 65 if(info.x<1 || info.x>200 || info.y<1 || info.y>200 || prime[map[info.x][info.y]]) 66 continue; 67 if(map[info.x][info.y]==Y) 68 return info.step; 69 if(!vis[info.x][info.y]){ 70 vis[info.x][info.y]=1; 71 q.push(info); 72 } 73 } 74 } 75 return -1; 76 } 77 78 int main(){ 79 80 //freopen("input.txt","r",stdin); 81 82 int cases=0; 83 getPrime(); 84 Graph(); 85 int si,sj; 86 while(~scanf("%d%d",&X,&Y)){ 87 int flag=1; 88 for(int i=1;i<=200 && flag;i++) 89 for(int j=1;j<=200 && flag;j++){ 90 if(map[i][j]==X){ 91 si=i; 92 sj=j; 93 flag=0; 94 } 95 } 96 int ans=BFS(si,sj,0); 97 if(ans==-1) 98 printf("Case %d: impossible\n",++cases); 99 else 100 printf("Case %d: %d\n",++cases,ans); 101 } 102 return 0; 103 }