我的LeetCode:https://leetcode-cn.com/u/ituring/
我的LeetCode刷题源码[GitHub]:https://github.com/izhoujie/Algorithmcii
LeetCode 999. 车的可用捕获量
题目
在一个 8 x 8 的棋盘上,有一个白色车(rook)。也可能有空方块,白色的象(bishop)和黑色的卒(pawn)。它们分别以字符 “R”,“.”,“B” 和 “p” 给出。大写字符表示白棋,小写字符表示黑棋。
车按国际象棋中的规则移动:它选择四个基本方向中的一个(北,东,西和南),然后朝那个方向移动,直到它选择停止、到达棋盘的边缘或移动到同一方格来捕获该方格上颜色相反的卒。另外,车不能与其他友方(白色)象进入同一个方格。
返回车能够在一次移动中捕获到的卒的数量。
示例 1:

输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出:3
解释:
在本例中,车能够捕获所有的卒。
示例 2:

输入:[[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出:0
解释:
象阻止了车捕获任何卒。
示例 3:
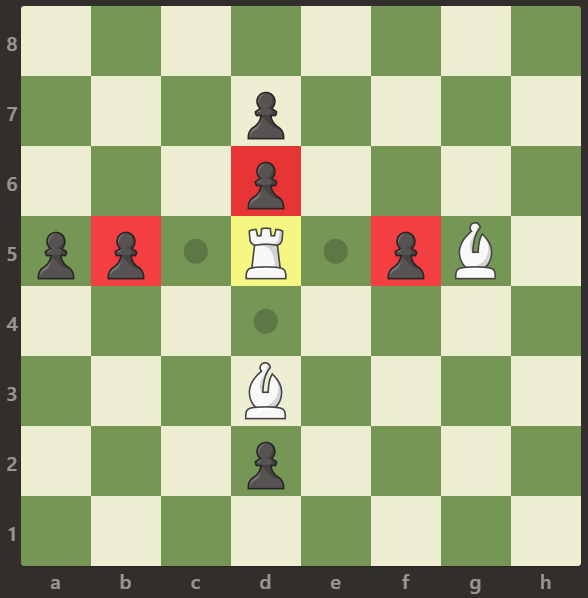
输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出:3
解释:
车可以捕获位置 b5,d6 和 f5 的卒。
提示:
- board.length == board[i].length == 8
- board[i][j] 可以是 'R','.','B' 或 'p'
- 只有一个格子上存在 board[i][j] == 'R'
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/available-captures-for-rook
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
思路1-题目较长,读懂后就简单了;
- 遍历找到R的位置;
- 从R的位置向四个方向上搜寻p,且p必须是首个遇到的字符,不能是B;
总结:本题的唯一难点就是题目又臭又长,读懂题比写代码要略难一点-。-
算法源码示例
package leetcode;
/**
* @author ZhouJie
* @date 2020年3月26日 下午1:21:57
* @Description: 999. 车的可用捕获量
*
*/
public class LeetCode_0999 {
}
class Solution_0999 {
/**
* @author: ZhouJie
* @date: 2020年3月26日 下午1:38:42
* @param: @param board
* @param: @return
* @return: int
* @Description: 1-
*
*/
public int numRookCaptures(char[][] board) {
// 四个方向的增量
int[] x = new int[] { 1, -1, 0, 0 };
int[] y = new int[] { 0, 0, -1, 1 };
// 可捕获的目标数;
int count = 0;
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 8; j++) {
// 找到R的位置
if (board[i][j] == 'R') {
// 在四个方向上探寻p
for (int k = 0; k < 4; k++) {
int x1 = i + x[k];
int y1 = j + y[k];
while (x1 > -1 && x1 < 8 && y1 > -1 && y1 < 8) {
if (board[x1][y1] == 'B') {
break;
} else if (board[x1][y1] == 'p') {
count++;
break;
} else {
x1 += x[k];
y1 += y[k];
}
}
}
return count;
}
}
}
return count;
}
}