作为西电学子,众所周知教学楼B楼设计十分复杂,对于初来乍到的新生十分不友好。很多混迹了四年的老油条也不擅长人脑导航,只能遍历每一层顺序寻找一间类似B520编号的教室。如何快速找到将要上课的教室?刚好有选修同学急需代码实现,苦于楼层构造稍显复杂,我便担此大任,简单完成了B楼教室辅助导航的小程序。
图与最短路算法
首先,定义B楼的图类型。
教室之间的连接形成的图是无向图,导航是区分方向的,因此需要保存相邻教室之间的方向关系。东西向:horizon,上下层:vertical。
无向图内部节点编号 0~v_num-1,教室、楼梯名称的外部标签为labels,需要vlookup映射回内部节点编号。
最后是Dijkstra算法,学过图论的话就很容易实现该代码。这里实现的为优先队列优化的(O((E+V)logV))复杂度算法。
class Graph:
def __init__(self, v_num=0, e_num=0, labels=None):
self.v_num = v_num # 节点数量
self.e_num = e_num # 边数量
self.g = [dict()]*v_num # 图结构,链表 g[u]: {v:distance}
self.node = [] # 节点名称,即教室编号、楼梯口编号等
self.horizon = set() # 保存东西关系节点对
self.vertical = set() # 保存上下关系节点对
if labels:
self.node = label
self.vlookup = dict(zip(self.node, range(self.v_num)))
else:
self.vlookup = dict()
def addNode(self, label):
v_id = self.v_num
self.node.append(label)
self.g.append(dict())
if label not in self.vlookup:
self.vlookup[label] = v_id
self.v_num += 1
# 图上两个节点添加一条边
# dire = 0 | walk | up
# 0: u==v
# walk: u->v 东西向
# up: u->u 上下楼
def addEdge(self, u, v, d, dire=0):
u_id = self.vlookup.get(u, -1)
v_id = self.vlookup.get(v, -1)
if u==-1 or v==-1:
print("节点不存在")
return
else:
self.g[u_id][v_id] = d
self.g[v_id][u_id] = d
# 记录相对位置
if dire=='walk':
self.horizon.add((u_id, v_id))
elif dire=='up':
self.vertical.add((u_id, v_id))
# 返回从起点到终点的最短路径
def dijkstra(graph, start, end):
start = graph.vlookup.get(start, -1)
end = graph.vlookup.get(end, -1)
if start==-1:
print("起点有误")
return
if end==-1:
print("教室编号不存在")
return
dis = [99999] * graph.v_num
path = [-1] * graph.v_num
vis = [False] * graph.v_num
from queue import PriorityQueue
pq = PriorityQueue()
dis[start] = 0
pq.put((0, start))
while pq.qsize()>0:
dis_now, u_now = pq.get()
if vis[u_now]:
continue
vis[u_now] = True
for v_to, dist_uv in graph.g[u_now].items():
if not vis[v_to] and dis_now + dist_uv < dis[v_to]:
dis[v_to] = dis_now + dist_uv
path[v_to] = u_now
pq.put((dis[v_to], v_to))
# 找到从 start 到 end的路径
route = [end]
pre = path[end]
while pre != start:
route.insert(0, pre)
pre = path[pre]
# print(pre, end=' <- ')
# 替换为外部标签
real_route = "从%s出发
" % ('通道口' + graph.node[start][2:]) if graph.node[start].startswith('st') else graph.node[start]
now = start
for u in route:
label = graph.node[u]
if label.startswith('st'):
label = '通道口' + label[2:]
elif label.endswith('x'):
now = u
continue
if (now, u) in graph.horizon:
real_route += "往西走到%s
" % label
elif (u, now) in graph.horizon:
real_route += "往东走到%s
" % label
elif (now, u) in graph.vertical:
real_route += "上楼走到%s
" % label
elif (u, now) in graph.vertical:
real_route += "下楼走到%s
" % label
else:
real_route += "走到%s
" % label
now = u
# real_route += " -> %s" % graph.node[u]
return real_route
B楼结构
没什么好说的,根据地图添加节点和相邻节点的边关系。
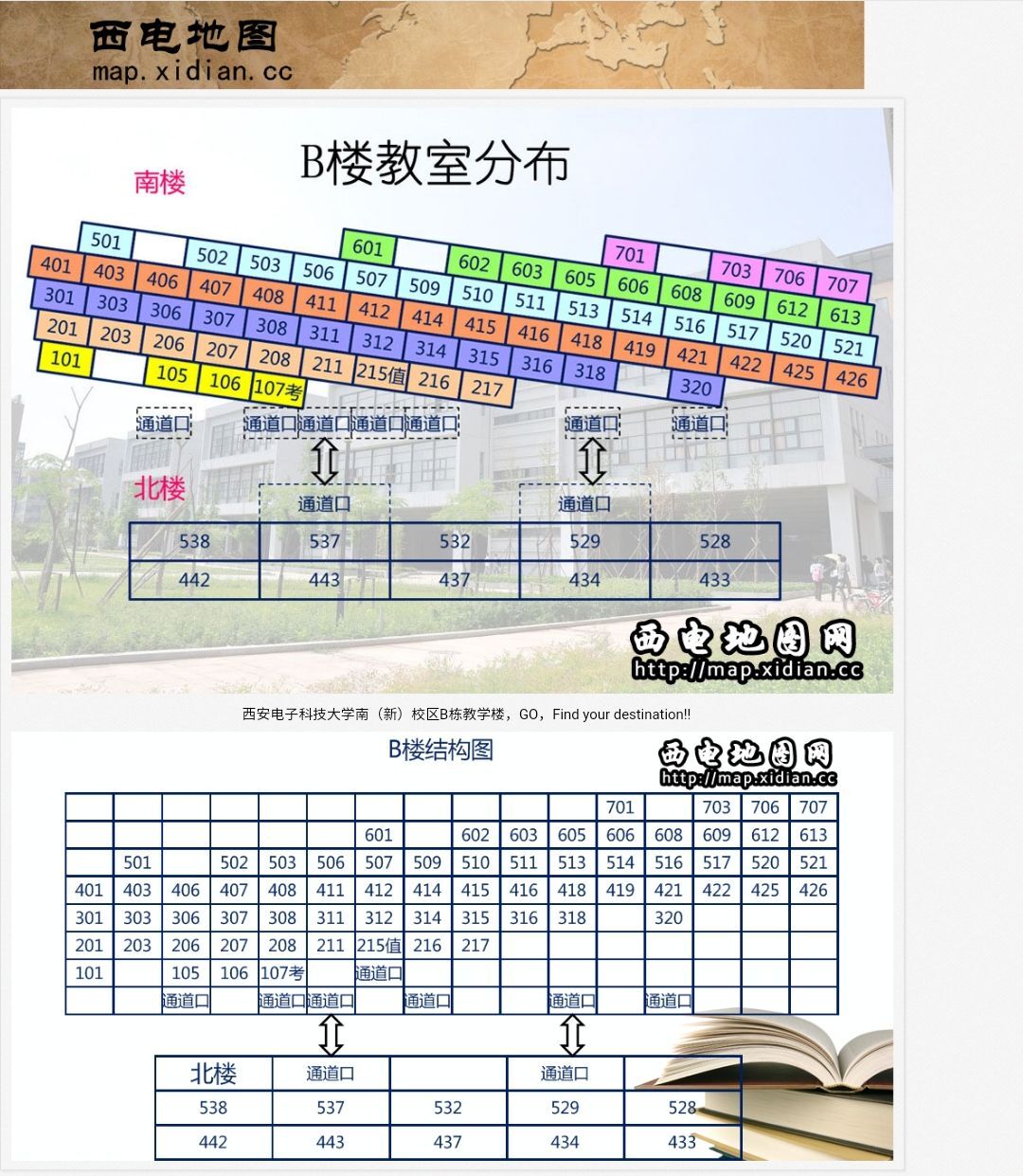
基本假设:
-
楼梯口与最近的教室门口视作同一节点(足够近,没必要分开);
-
不考虑走后门进教室(相邻教室的前后门可以当作在一起);
那么只需要在B楼最东端添加一列节点即可。
共有六个通道口作为起始点。
from alg import Graph
# 楼梯分布情况
# | - - - - - - | - | - - - - | - - - - - |
# 东<--->西
# 教室门朝向西,假设不从后门进入,因此增加东边楼梯的节点,西边楼梯直接表示为教室节点
# level0:入口层, st1~st6 六个入口
# ??x 未编号教室
# |ab 楼梯 a为楼梯编号 0~6 b为楼层
# st? 地面层楼梯入口
# --- 没有教室
level0 = ['---', '---', '---', 'st1', '01x', 'st2', 'st3', '02x', 'st4', '03x', '04x', 'st5', '05x', 'st6', '---', '---', '---']
level1 = ['|01', '101', '10x', '105', '106', '107']
level2 = ['|02', '201', '203', '206', '207', '208', '211', '215', '216', '217']
level3 = ['|03', '301', '303', '306', '307', '308', '311', '312', '314', '315', '316', '318', '31x', '320']
level4 = ['|04', '401', '403', '406', '407', '408', '411', '412', '414', '415', '416', '418', '419', '421', '422', '425', '426']
level5 = ['|05', '50x', '501', '|15', '502', '503', '506', '507', '509', '510', '511', '513', '514', '516', '517', '520', '521']
level6 = ['---', '---', '---', '---', '---', '---', '|36', '601', '60x', '602', '603', '605', '606', '608', '609', '612', '613']
level7 = ['---', '---', '---', '---', '---', '---', '---', '---', '---', '---', '---', '|57', '701', '|67', '703', '706', '707']
nodes = [level0, level1, level2, level3, level4, level5, level6, level7]
# graph.append(level1, level2)
# 教室间距
span_distance = 10
# 楼层高度
height = 4
def initGraph():
graph = Graph()
for l in nodes:
for v in l:
graph.addNode(v)
# print(graph.node)
# print(graph.vlookup)
# 每层连边
for l in nodes:
for i in range(1, len(l)):
if l[i-1]!='---' and l[i]!='---':
graph.addEdge(l[i-1], l[i], span_distance, 'walk')
# 上下连边
# st1 105相连
# st2 107相连
# st3 211相连
# st4 上楼 312
# st5 318相连
# st6 320相连
graph.addEdge('st1', '105', 0)
graph.addEdge('st2', '107', 0)
graph.addEdge('st3', '211', height/2, 'up')
graph.addEdge('st4', '312', height, 'up')
graph.addEdge('st5', '318', 0)
graph.addEdge('st6', '320', 0)
# 楼梯
graph.addEdge('|01', '|02', height, 'up')
graph.addEdge('|02', '|03', height, 'up')
graph.addEdge('|03', '|04', height, 'up')
graph.addEdge('|04', '|05', height, 'up')
graph.addEdge('105', '206', height, 'up')
graph.addEdge('206', '306', height, 'up')
graph.addEdge('306', '406', height, 'up')
graph.addEdge('406', '|15', height, 'up')
graph.addEdge('107', '208', height, 'up')
graph.addEdge('208', '308', height, 'up')
graph.addEdge('308', '408', height, 'up')
graph.addEdge('408', '503', height, 'up')
graph.addEdge('211', '311', height, 'up')
graph.addEdge('311', '411', height, 'up')
graph.addEdge('411', '506', height, 'up')
graph.addEdge('506', '|36', height, 'up')
graph.addEdge('312', '412', height, 'up')
graph.addEdge('412', '507', height, 'up')
graph.addEdge('507', '601', height, 'up')
graph.addEdge('318', '418', height, 'up')
graph.addEdge('418', '513', height, 'up')
graph.addEdge('513', '605', height, 'up')
graph.addEdge('605', '|57', height, 'up')
graph.addEdge('320', '421', height, 'up')
graph.addEdge('421', '516', height, 'up')
graph.addEdge('516', '608', height, 'up')
graph.addEdge('608', '|67', height, 'up')
# print(graph.g)
# 北楼
# st3 443 地面层相连
# st5 434 地面层相连
Nlevel4 = ['442', '443', '437', '434', '433']
Nlevel5 = ['538', '537', '532', '529', '528']
for v in Nlevel4:
graph.addNode(v)
for v in Nlevel5:
graph.addNode(v)
# 连边
for i in range(1, len(Nlevel4)):
graph.addEdge(Nlevel4[i-1], Nlevel4[i], span_distance*3, 'walk')
for i in range(1, len(Nlevel5)):
graph.addEdge(Nlevel5[i-1], Nlevel5[i], span_distance*3, 'walk')
# 上下楼梯
graph.addEdge('st3', '443', height, 'up')
graph.addEdge('st5', '434', height, 'up')
graph.addEdge('443', '537', height, 'up')
graph.addEdge('434', '529', height, 'up')
# 忽略南北楼之间的连接
# 需要实地考察 哪几间是相邻的
return graph
测试与结果
简单写一个调用入口吧
from alg import dijkstra
from map import initGraph
if __name__ == '__main__':
graph = initGraph()
# print(graph.g)
# print(graph.vlookup)
path = dijkstra(graph, 'st3', '426')
print(path)
运行结果:
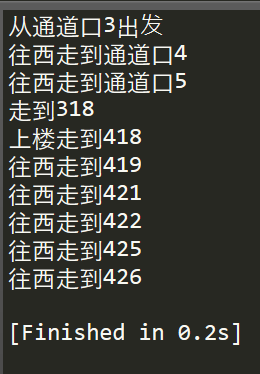
能造福将来的西电学子,也是做了一点微小的工作 .
(完)