[算法]最短路算法

最短路算法用于求带权有向图中，两点之间的最近距离。它通过不断扩大已知的最短路径，直到最短路径覆盖终点为止。由下面的程序可以看书，它的时间复杂度为O(n^3)。下面举一简单例子说明最短路算法的步骤。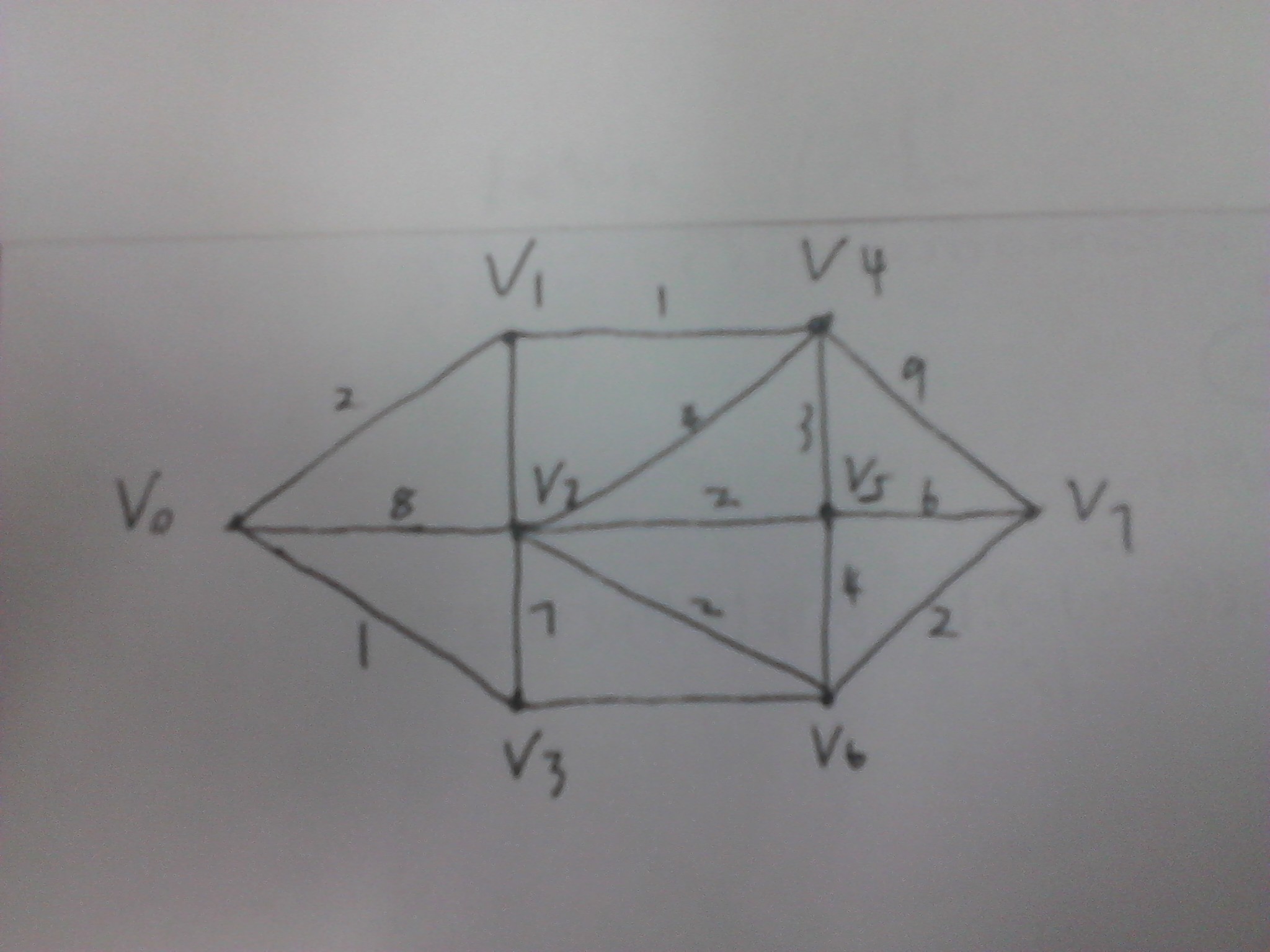

想求v0到v7的最短路径，初始的时候，只知道v0距离自己的最短距离为0.

使用一个close数组存储以求得与v0的最短距离，如未求得的复制为-1. 开始时，close[0]=0;

(1)遍历close里面的点，找出所有与close点相邻但不在close里面的点。

刚开始只有v0在close里面，与它相邻的点有v1、v2、v3。

(2)找出这些点中，距离v0最近的一个点。

例如点i是close里面的点，j是i的邻接点，那么j与v0的最近距离=ij距离+i与v0的最短距离。由于i是close里面的点，i与

v0的最短距离已知，就是close[i]。

此时v3距离v0距离为close[0]+1，比v2和v1都小，因此v3选入close，close[3]=1。最短路径的范围已经扩大到v0到v3.

(3)此时，与v0-v3这一段已知最短路相邻的点有v1v2v6，v1距离v0最短距离=2，v6最短距离=v3到v6距离9（图漏写了）+close[3]=10，v2到v0的距离显然是8.因此，这三个点中距离v0最短的点是v1，因此v1收入close，close[1]=1。此时，已知最短路的范围已经扩到到v1-v0-v3.

一直重复，每次加入一个与close（或者说是已知最短路）相邻的点，直到要求的终点加入close就求得起点到终点的最短路。

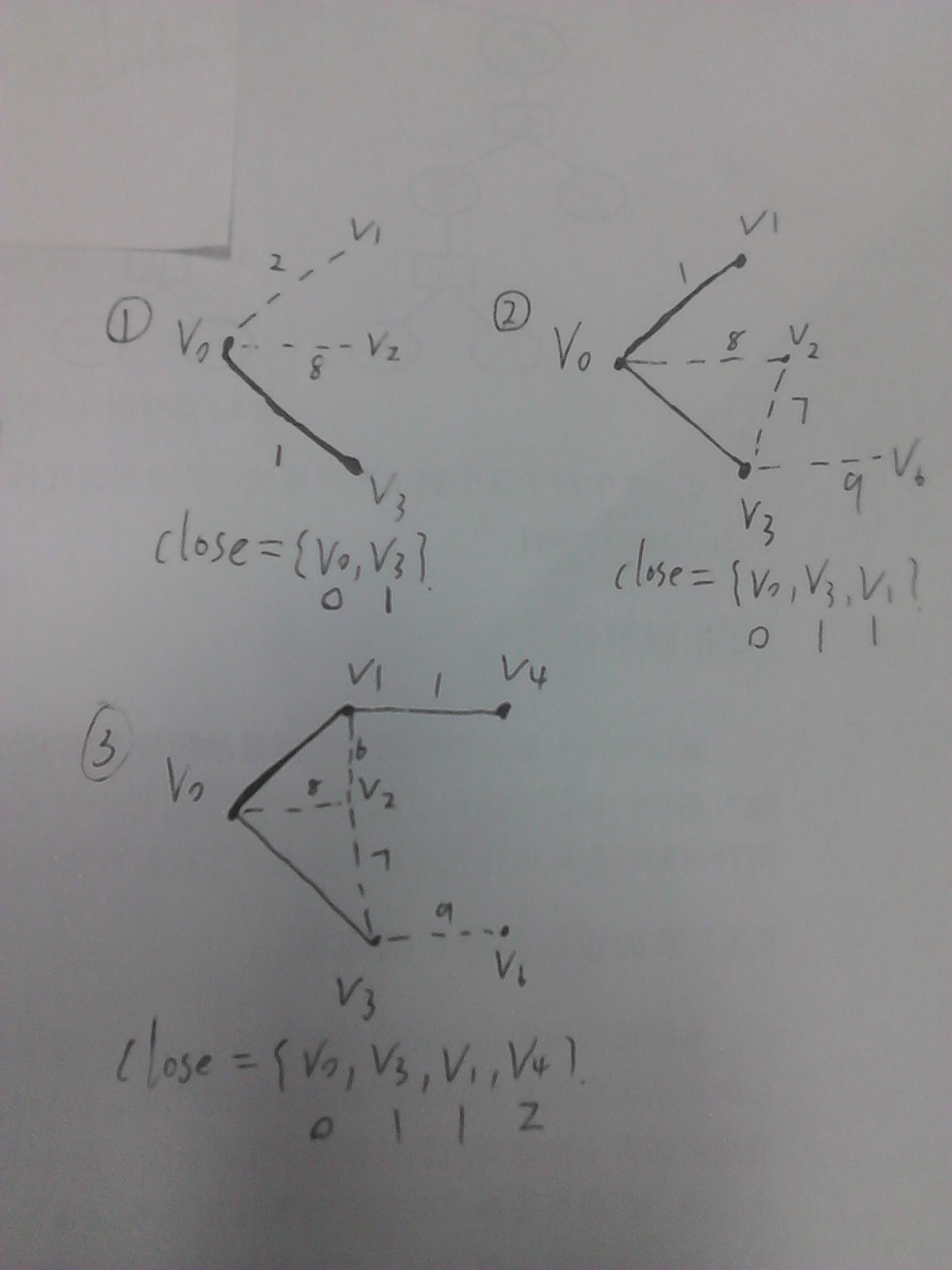
整个最短路算法，其实就是一个最优路径不断扩大的过程，一开始只有一个起点，然后每次添加一个与起点距离最短的邻接点，直到找到终点位置。上图展示了扩展的过程，图1从v0扩展到v3.图2扩展到v1-v0-v3，图3扩展到v4-v1-v0-v3.

下面是代码：

int minpath(){
    int matrix[8][8]={//邻接矩阵，不相连的为0，非0表示两点之间的距离
        {0,2,8,1,0,0,0,0},
        {2,0,6,0,1,0,0,0},
        {8,6,0,7,4,2,2,0},
        {1,0,7,0,0,0,9,0},
        {0,1,4,0,0,3,0,9},
        {0,0,2,0,3,0,4,6},
        {0,0,2,9,0,4,0,2},
        {0,0,0,0,9,6,2,0}};
    int close[8];//存放已经找到与第一个点最短短的点，数组的值是改点与起点的最短距离
    int i,j;
    close[0]=0;//起点距离自己的距离为0
    for(i=1;i<8;++i)
        close[i]=-1;//没找到的设为-1
    while(close[7]==-1){//最后一个点为想找的终点
        int min=0x7fffffff;//记录暂时找到的最小距离，初始化为最大的int
        int imin;//记录得到最小值的点
        for(i=0;i<8;++i){
            if(close[i]!=-1){//遍历close里面的点的所有邻接且不在close内的点
                for(j=0;j<8;++j){
                    if(close[j]==-1 && matrix[i][j]!=0 && matrix[i][j]+close[i]<min){
                        min=matrix[i][j]+close[i];//ij的距离加上i到起点的最短距离就是j到起点的最短距离
                        imin=j;
                    }
                }
            }
        }
        close[imin]=min;//所有相邻非close点中，与起点最近的点加入close
    }
    return close[7];
}