http://www.lydsy.com/JudgeOnline/problem.php?id=1662
这道题折腾了我两天啊~!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
果然还是太弱
!!!!!!!!!!
一直想不通啊。。
数位dp太神了
。。orz
看题解各种不会啊。。。(神犇们的题解都说,裸数位dp,没了QAQ)
参考论文 刘聪《浅谈数位类统计问题》
在信息学竞赛中,有这样一类问题:求给定区间中,满足给定条件的某个 D 进制数或此类数的数量。所求的限定条件往往与数位有关,例如数位之和、指定数码个数、数的大小顺序分组等等。题目给定的区间往往很大,无法采用朴素的方法求解。此时,我们就需要利用数位的性质,设计 log(n)级别复杂度的算法。解决这类问题最基本的思想就是“逐位确定”的方法。
比如在本题中,要求求区间l-r中二进制表达式中0比1大的数字的个数,且本题区间满足区间减法,因此可以进一步简化问题:令 count[i..j]表示[i..j]区间内合法数的个数,则 count[i..j]=count[0..j]-count[0..i-1]。换句话说,给定 n,我们只需求出从 0 到 n 有多少个符合条件的数。
我们将所有的数想象成一颗按位建的完全二叉树
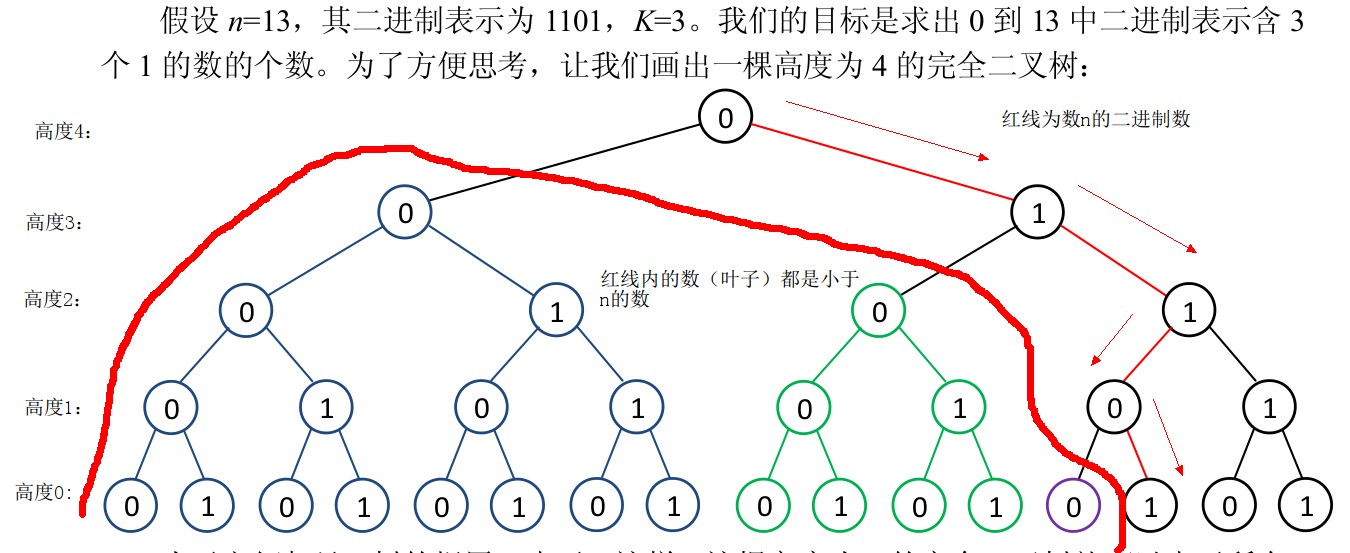
为了方便起见,树的根用 0 表示。这样,这棵高度为 4 的完全二叉树就可以表示所有 4位二进制数(0..2 4 -1),每一个叶子节点代表一个数。其中,红色路径表示 n。所有小于 n 的数组成了三棵子树,分别用蓝色、绿色、紫色表示。因此,统计小于 13 的数,就只需统计这三棵完整的完全二叉树。
高度一定不要弄错!!!
比如二进制1101,那么高度为4,高度为0就是叶子!也就是一片叶子对应一个数!
还有,0是根!不要弄错,对,0是根!
每一颗子完全二叉树的0都是根!除了叶子
那么现在问题转为怎么求这个。
我们设f(k, x, y)表示k高度x个0,y个1的方案数(这里我不敢递推,很难理解,等以后再来看看。我这里就用记忆化搜索了,较容易理解)(这里还有2个隐式的状态,即在n这个数的路径和这个状态是否为根)
那么对于每个状态,我们首先考虑隐式状态。假设现在从根0开始遍历,高度为k,左子树是一棵以0为根的子树,右子树是以1为根的子树,那么我们要考虑n的二进制的第(k-1)位,如果(k-1)位是0,那么只能遍历左子树,否则2棵子树都能遍历。(这个前提是在这个状态仅当在n这个数的路径上!)
而向左子树遍历时,又相应进入一颗完全二叉树,那么可以重新计数。(重要!)
而右子树遍历时,就不能重新计数了(重要!)
就要根据状态进行转移,即y+1
考虑重复计算多次,那么我们需要记忆化,否则tle
什么时候才记忆化呢,当且仅当这个状态不是以0为根的树的根,也不是n的数的路径时,才要记忆化。
。。
多考虑下,具体细节写在代码里
#include <cstdio>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, n) for(int i=0; i<(n); ++i)
#define for1(i,a,n) for(int i=(a);i<=(n);++i)
#define for2(i,a,n) for(int i=(a);i<(n);++i)
#define for3(i,a,n) for(int i=(a);i>=(n);--i)
#define for4(i,a,n) for(int i=(a);i>(n);--i)
#define CC(i,a) memset(i,a,sizeof(i))
#define read(a) a=getint()
#define print(a) printf("%d", a)
#define dbg(x) cout << #x << " = " << x << endl
#define printarr(a, n, m) rep(aaa, n) { rep(bbb, m) cout << a[aaa][bbb]; cout << endl; }
inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }
inline const int max(const int &a, const int &b) { return a>b?a:b; }
inline const int min(const int &a, const int &b) { return a<b?a:b; }
const int BIT=32;
int f[BIT][BIT][BIT], s[BIT];
int dfs(int x, int x1, int x2, bool first, bool line) {
if(!x) {
if(first) return 1; //要考虑0这个状态,也可以不考虑,因为此时x1和x2都等于0
if(x1>=x2) return 1;
return 0;
}
if(!first && !line && f[x][x1][x2]!=-1) return f[x][x1][x2]; //当隐式条件都不满足时才能记忆化
int last=1, tot=0; if(line) last=s[x]; //当这个状态在n这个数的路径上
for1(i, 0, last) {
if(first) { //当这个状态是根
if(!i) tot+=dfs(x-1, 0, 0, 1, line && (last==i)); //遍历左子树,重新计数,并且判断是否在n这个数的路径上
else tot+=dfs(x-1, x1, x2+1, 0, line && (last==i));
}
else {
if(!i) tot+=dfs(x-1, x1+1, x2, 0, line && (last==i));
else tot+=dfs(x-1, x1, x2+1, 0, line && (last==i));
}
}
if(!first && !line) f[x][x1][x2]=tot; //同之前的记忆化
return tot;
}
int sum(int x) {
int len=0;
while(x) {
s[++len]=x&1;
x>>=1;
}
return dfs(len, 0, 0, 1, 1);
}
int main() {
int l=getint(), r=getint();
CC(f, -1);
print(sum(r)-sum(l-1));
return 0;
}
Description
正 如你所知,奶牛们没有手指以至于不能玩“石头剪刀布”来任意地决定例如谁先挤奶的顺序。她们甚至也不能通过仍硬币的方式。 所以她们通过"round number"竞赛的方式。第一头牛选取一个整数,小于20亿。第二头牛也这样选取一个整数。如果这两个数都是 "round numbers",那么第一头牛获胜,否则第二头牛获胜。 如果一个正整数N的二进制表示中,0的个数大于或等于1的个数,那么N就被称为 "round number" 。例如,整数9,二进制表示是1001,1001 有两个'0'和两个'1'; 因此,9是一个round number。26 的二进制表示是 11010 ; 由于它有2个'0'和 3个'1',所以它不是round number。 很明显,奶牛们会花费很大精力去转换进制,从而确定谁是胜者。 Bessie 想要作弊,而且认为只要她能够知道在一个指定区间范围内的"round numbers"个数。 帮助她写一个程序,能够告诉她在一个闭区间中有多少Hround numbers。区间是 [start, finish],包含这两个数。 (1 <= Start < Finish <= 2,000,000,000)
Input
* Line 1: 两个用空格分开的整数,分别表示Start 和 Finish。
Output
* Line 1: Start..Finish范围内round numbers的个数
Sample Input
Sample Output
输出解释:
2 10 1x0 + 1x1 ROUND
3 11 0x0 + 2x1 NOT round
4 100 2x0 + 1x1 ROUND
5 101 1x0 + 2x1 NOT round
6 110 1x0 + 2x1 NOT round
7 111 0x0 + 3x1 NOT round
8 1000 3x0 + 1x1 ROUND
9 1001 2x0 + 2x1 ROUND
10 1010 2x0 + 2x1 ROUND
11 1011 1x0 + 3x1 NOT round
12 1100 2x0 + 2x1 ROUND