最小成本排序——置换群

给你一个序列s = {a1,a2……an}，然后可以任意交换其中两个元素 i , j 的位置，代价是ai + aj，把序列变成有序，求最小代价

思路：置换群的巧妙应用 

以4 3 2 7 1 6 5为例画图

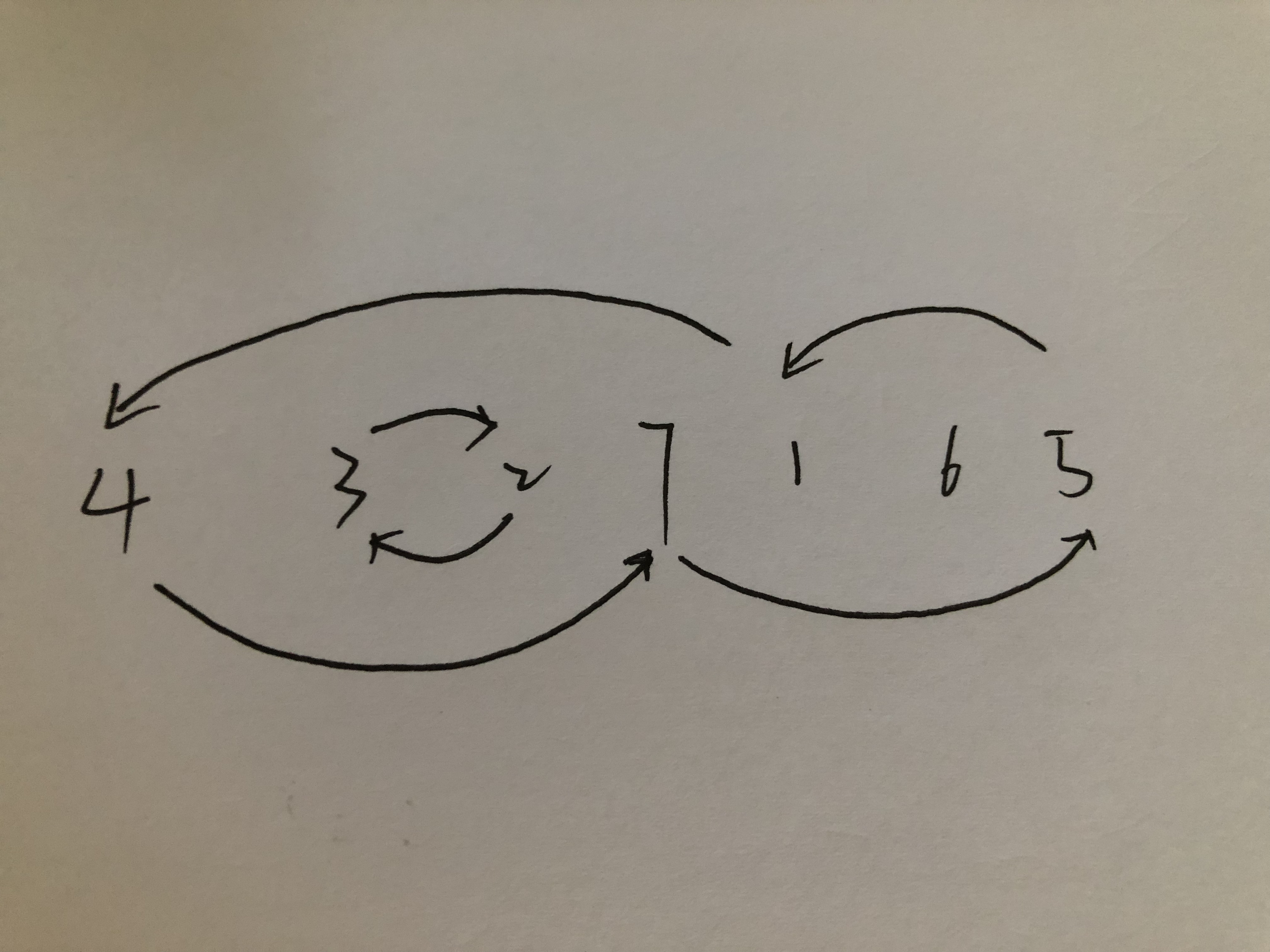
有三个环

4->7->5->1->4

3->2->3

6->6

要求代价最小，则通过用环里的最小的元素来移动其他元素

成本为：Σwi+(n-2)*min(wi)

求出每个环的代价后相加就是成本

但也存在反例，有时可以通过借用环外的元素使成本更低

借用成本所增加的成本为：2*(min(wi)+x) //x为整个序列的最小元素 

节约的成本为：(n-1)*(min(wi)-x)

这时候总成本为：Σwi+(n-2)*min(wi)+2*(min(wi)+x)-(n-1)*(min(wi)-x)=Σwi+min(wi)+(n+1)*x

总结：求最小成本应考虑借整体最小元素与不借元素两种情况

#include <iostream>
#include <algorithm>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 100100;
int a[maxn], b[maxn], T[maxn], n, minn;
bool vis[maxn];
int solve() {
    int ans = 0;
　　//枚举每个环
    for (int i = 0; i < n; i++) { 
        if (vis[i]) continue;
        int cur = i,sum = 0;
        int mini = inf;
        int k = 0;
        while (1) {
            k++;
            vis[cur] = 1;
            int v = a[cur];
            sum += v;
            mini = min(mini, v);
            cur = T[v];
            if (vis[cur]) break;
        }
        ans += min(sum + (k - 2) * mini, mini + sum + (k + 1) * minn);
    }
    return ans;
}
int main() {
    cin >> n;
    minn = inf;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        b[i] = a[i];
        vis[i] = 0;
        minn = min(minn, a[i]);
    }
    sort(b, b + n);
    for (int i = 0; i < n; i++) T[b[i]] = i;
    int ans = solve();
    cout << ans << endl;
    return 0;
}

例题：http://poj.org/problem?id=3270