【剑指Offer】矩形覆盖

题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

解法1

一开始尝试解这道题的时候其实有些不知道怎么下手，花了很长时间。后来才发现可以利用递归的思想，将n的值不断放小到某个可以直接知道结果的值。虽然直接实现递归的算法可能效率不高，但在找到题目的递归解法后，再在递归算法的基础上做优化，就可以得到一个满意的答案。
回到本题，用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，假设有F(n)种方法
先用一个2*1的小矩形，竖着覆盖大矩形，如下图所示。则还剩下2*(n-1)的大矩形需要覆盖，即有F(n-1)种方法

如果先用一个2*1的小矩形，横着覆盖大矩形，如下图所示。则底部的红色区域也只能用一个2*1的小矩形横着覆盖。则还剩下2*(n-2)的大矩形需要覆盖，即有F(n-2)种方法

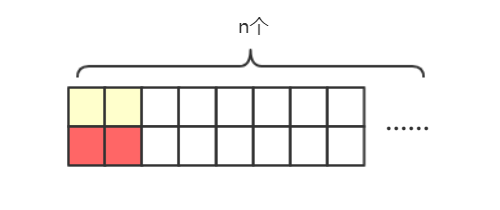
由以上两种情况可知，F(n) = F(n - 1) + F(n - 2)，我们只需要知道F(0)，F(1)，就可以求得F(n)。很明显这是一个斐波那契数列的定义。对于斐波那契数列的多种求解方法可以参考【剑指Offer】斐波那契数列
当n = 0的时候，显然有0中覆盖方法，即F(0) = 0
当n = 1的时候，只有一种覆盖方法，即F(1) = 1
我们可以直接使用直观的递归算法求解，如下所示

实现代码

public int rectCover(int number)
{
    if (number <= 0)
        return 0;
    if (number == 1)
        return 1;
    else if (number == 2)
        return 2;
    return rectCover(number - 1) + rectCover(number - 2);
}

解法2

可以使用循环迭代的方式优化递归算法，如下所示

实现代码

public int rectCoverOptimize(int number)
{
    int f = 0, g = 1;
    while (number-- > 0)
    {
        g = f + g;
        f = g - f;
    }
    return f == 0 ? 0 : g;
}

解法3

既然已经知道本题实际上就是求解斐波那契数列，那么可以利用矩阵的快速幂求解

实现代码

// 矩阵乘法
public int[,] matrixMul(int[,] m1, int[,] m2)
{
    int[,] ret = {
        {m1[0, 0] * m2[0,0] + m1[0, 1] * m2[1,0], m1[0, 0] * m2[0,1] + m1[0, 1] * m2[1,1]}, 
        {m1[1, 0] * m2[0,0] + m1[1, 1] * m2[1,0], m1[1, 0] * m2[0,1] + m1[1, 1] * m2[1,1]}
    };
    return ret;
}

// 矩阵快速幂
public int[,] matrixPow(int[,] m, int n)
{
    int[,] ret = { { 1, 0 }, { 0, 1 } };
    while (n > 0)
    {
        if ((n & 1)> 0){
            ret = matrixMul(ret, m);
        }
        n >>= 1;
        m = matrixMul(m, m);
    }
    return ret;
}

public int rectCoverOptimize2(int number)
{
    if (number == 0)
        return 0;
    int[,] unit = { { 1, 1 }, { 1, 0 } };
    int[,] ret = matrixPow(unit, number);
    int[,] m = { { 1, 0 }, { 0, 0 } };
    ret = matrixMul(ret, m);
    return ret[0,0];
}

更多题目的完整描述，AC代码，以及解题思路请参考这里