iwehdio的博客园:https://www.cnblogs.com/iwehdio/
1、快排
-
快速排序:
-
将子序列划分为两个部分S1、S2,并且满足S1中最大值小于S2中最小值。
-
这样,在子序列分别递归的排序之后,原序列自然有序。
-
轴点:左 / 右侧的元素,均不比它更大 / 小。
-
轴点自然的将序列分为了符合之前条件的两个部分,剩下的部分只需递归完成即可。
template <typename T> void Vector<T>::quickSort ( Rank lo, Rank hi ) { if ( hi - lo < 2 ) return; //单元素区间自然有序,否则... Rank mi = partition ( lo, hi ); //在[lo, hi)内构造轴点 quickSort ( lo, mi ); //对前缀递归排序 quickSort ( mi + 1, hi ); //对后缀递归排序 } -
但是,轴点在原始序列中未必存在。轴点存在的必要条件是,轴点在序列中所在的位置必定是其排序后所在的位置(就位)。
-
在有序序列中,所有元素都是轴点。因此快排就是将所有元素逐个转换为轴点的过程。通过适当的交换,可使任一元素转换为轴点。
-
轴点的构造:
-
以首元素m为轴点为例,使用lo和hi两个指针,将序列分为三部分。L是从前往后的小于等于m的部分,G是从后往前的大于等于m的部分,U是未扫描的部分。lo和hi指向U的边界。
-
lo和hi向中间扫描,最终重合的位置就是m作为轴点所在的位置。

-
具体的,在算法进行的开始,先去除m并备份。这样原来m的位置就空闲了,并由lo指向。
-
然后hi开始扫描,遇到大于等于m的就越过,遇到小于m的就将其移至lo指向的空闲位置。然后改为lo扫描,hi空闲。
-
最后扫描完成后,将备份的m移入空闲位置。
-
-
时间复杂度最好O(nlog n),最坏O(n^2),平均O(nlog n)。
-
-
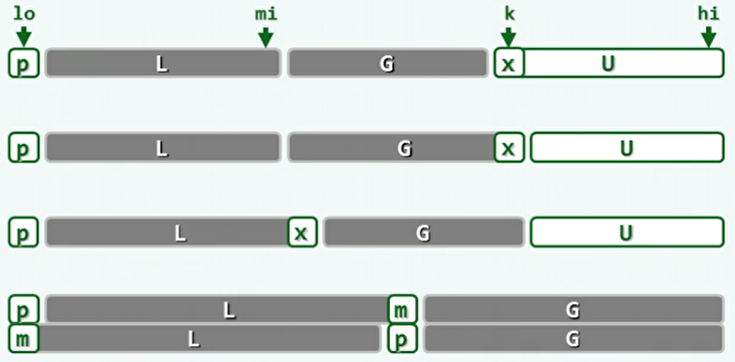
快速排序的变种:
- 同样的将整个序列分为四部分,只不过待处理部分U在最后端,而P也不需要取出备份。
- k指针从头后移,遇到大于等于轴点的元素就只后移,相当于将该元素归入G。遇到小于轴点的元素,则与G中的首元素交换位置,相当于将该元素归入L,然后再后移。
- 最后U的规模为0时,将位于序列首端的轴点P与L中的最后一个元素交换位置。
-
实现:
template <typename T> //轴点构造算法:通过调整元素位置构造区间[lo, hi)的轴点,并返回其秩 Rank Vector<T>::partition ( Rank lo, Rank hi ) { //版本C swap ( _elem[lo], _elem[ lo + rand() % ( hi - lo ) ] ); //任选一个元素与首元素交换 T pivot = _elem[lo]; //以首元素为候选轴点——经以上交换,等效于随机选取 int mi = lo; for ( int k = lo + 1; k < hi; k++ ) //自左向右扫描 if ( _elem[k] < pivot ) //若当前元素_elem[k]小于pivot,则 swap ( _elem[++mi], _elem[k] ); //将_elem[k]交换至原mi之后,使L子序列向右扩展 swap ( _elem[lo], _elem[mi] ); //候选轴点归位 return mi; //返回轴点的秩 }
2、选取
-
众数:这里指的是出现次数超过序列长度一半以上的元素。
-
这种定义下,如果存在众数,则其必然也是中位数。
-
减而治之:
- 若在向量A的前缀P(P长度为偶数)中,元素x出现的次数恰占半数,则A有众数仅当,对应的后缀A –Р有众数m,且m就是A的众数。
- 若x= m,则在排除前缀P之后,m与其它元素在数量上的差距保持不变。
- 若x ≠ m,则在排除前缀Р之后,m与其它元素在数量上的差距不致缩小。

-
实现:
- 用一个计数器记录众数的候选者与其他元素的数量差。
template <typename T> T majEleCandidate ( Vector<T> A ) { //选出具备必要条件的众数候选者 T maj; //众数候选者 // 线性扫描:借助计数器c,记录maj与其它元素的数量差额 for ( int c = 0, i = 0; i < A.size(); i++ ) if ( 0 == c ) { //每当c归零,都意味着此时的前缀P可以剪除 maj = A[i]; c = 1; //众数候选者改为新的当前元素 } else //否则 maj == A[i] ? c++ : c--; //相应地更新差额计数器 return maj; //至此,原向量的众数若存在,则只能是maj —— 尽管反之不然 } -
选取的通用算法:
-
选取的目标是,取出序列中经排序后秩为k的元素。
-
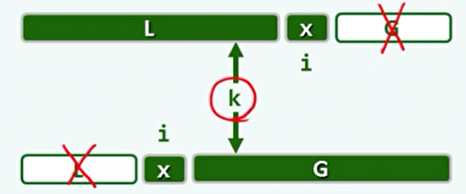
quickSelect():
- 借鉴快排的思想,如果轴点的秩恰好为k,则直接返回。
- 如果轴点的秩不是k,但可通过与轴点的秩比较,得出k是在L中还是在G中。
-
linearSelect():
- 设定一个常量Q,当序列A短于Q时,则为递归基,使用平凡的选取算法(比如排序)。
- 否则,将序列分为n/Q个长为Q的序列。
- 对于每个序列进行排序,并选出各自的中位数。递归的选取出这些中位数的中位数,记为M。
- 将整个序列分为,L:小于M的;E:等于M的;G:大于M的。
- 如果目标的秩k落在L或G,则递归,若落在E则返回M。
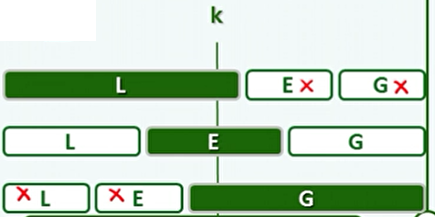
- 对于M,至少各有n/4个元素,不小于 / 不大于M。即白色部分占n/4,且必然大于等于M,黑色部分占n/4,且必然小于等于M。

- 时间复杂度与Q的取值有关,至少应大于4。时间复杂度O(n)。
-
3、希尔排序
- 希尔排序:
- 将整个序列视为一个矩阵,逐列各自排序。矩阵的宽度逐渐缩减,最后变成一列。对于分为h列的排序,称为h-sorted。
- 需要一个步长序列,存储了矩阵的宽度变化。
- 对于每一列的排序算法,需要使用输入敏感的算法,以保证在有序性持续改善的情况下,计算成本较低。
- 有序性可以通过逆序对的数量表征。
- shell序列:
- 从1开始,以2为比的等比数列。
- 因为除了第一项都是偶数,因此两次分列时没有进行元素的交换。
- 应该尽量使得相邻的列数互质。
- 如果一个序列中有,s[i]<=s[i+g],则称为这个序列为g-ordered。
- 已经证明,对于一个g-ordered序列,经过h-sorted后,依然是g-ordered的。
- 这就说明了希尔排序在不同宽度的列进行排序后,会成为所有矩阵宽度的h-ordered。
- 而且所有h-ordered的序列,都是可以线性组合的。
- 又因为,对于互质的数g和h,其无法完成线性组合的最大值为gh-g-h。
- 因此对于一个h-ordered和g-ordered序列,s[i]的逆序对只可能存在于其后的(g-1)(h-1)个位置内。这个范围会在排序过程中逐渐缩减。最终用于插入排序的序列逆序对很少。
4、十大排序算法
-
学习自:十大经典排序算法。
-
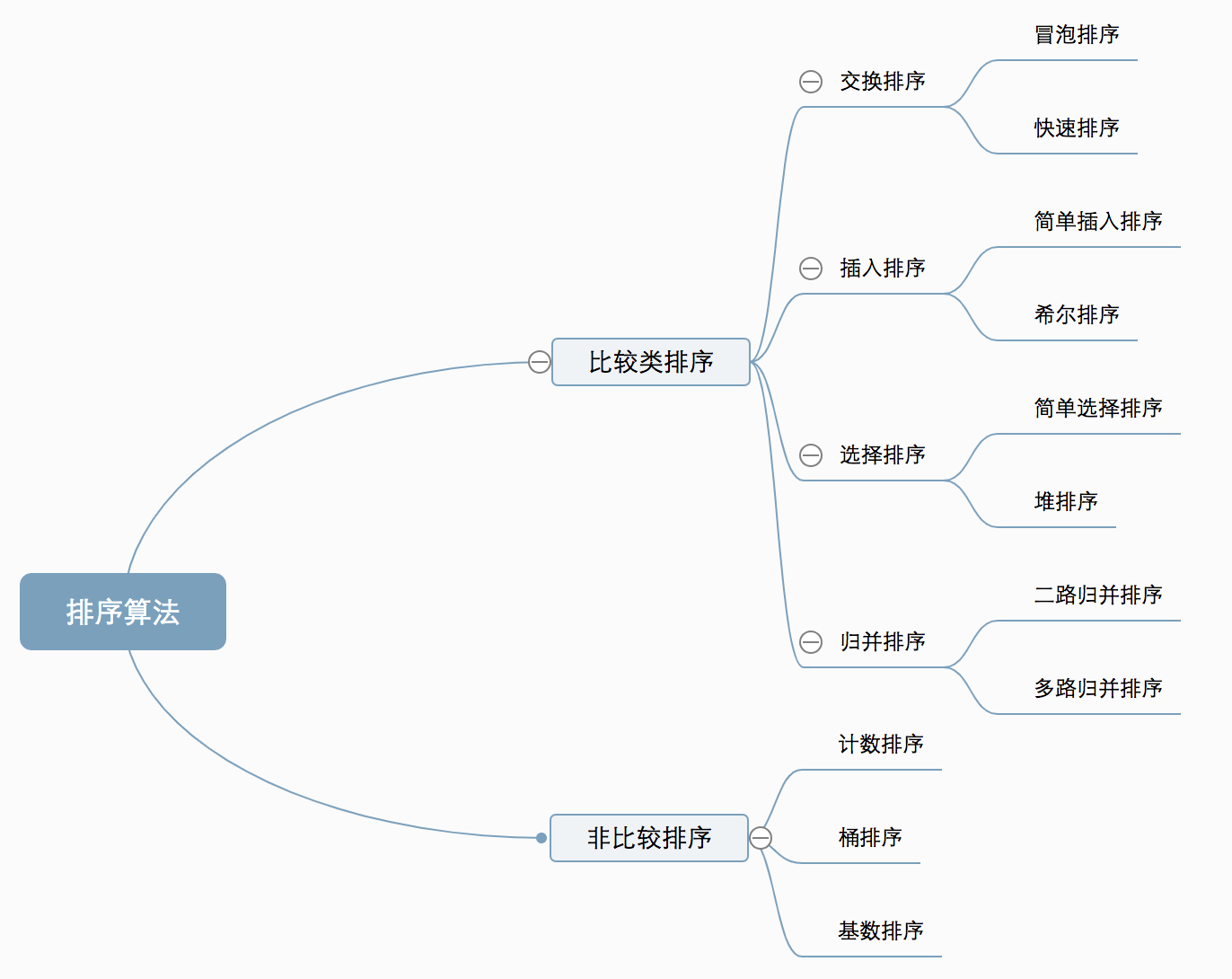
排序算法分类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlog n),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
-
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
-
不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面。
-
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
-
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。

冒泡排序Bubble
-
描述:
- 比较相邻的两个元素,如果后边的元素较大则交换位置。
- 从前往后扫描,n次扫描后这样最大的n个元素必然位于最后。
- 设置一个标志位,如果这次扫描没有发生交换则说明排序完成。
- 用一个递增变量i来记录扫描次数,不扫描最后的有序部分。
-
实现:
int temp; for (int i = 0; i < arr.length; i++) { for (int j = 0; j < arr.length-1-i; j++) { if (arr[j] > arr[j+1]) { temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } //----------------------------------- boolean flag = true; //用于在没有发生交换时提前退出 int j=arr.length; //用于每次扫描不遍历有序部分 int temp; while (flag) { flag = false; for (int i = 0; i < j-1; i++) { if (arr[i] > arr[i+1]) { temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; flag = true; } } j--; }
选择排序Selection
-
描述:
- 以有序序列在尾部为例(这样每次扫描从头开始),每次选择无序部分最大的元素,存放在有序部分的最后。
- 用一个指针记录有序序列下一个插入位置,另一个指针进行扫描。
-
实现:
int max; //记录最大值及其位置 int index; for (int i = arr.length-1; i >=0; i--) { //从后往前,插入位置 max = arr[i]; index = i; for (int j = 0; j <= i; j++) { //从前往后扫描 if (max < arr[j]){ max = arr[j]; index = j; } } arr[index] = arr[i]; arr[i] = max; }
插入排序Insertion
-
描述:
- 以有序序列在前为例,从前往后扫描,将元素插入到有序序列中的合适位置。
- 该元素从后往前与有序序列中的元素比较,如该元素较小则有序序列中的元素后移一位。
-
实现:
int j; int temp; for (int i = 1; i < arr.length; i++) { //从前往后扫描 temp = arr[i]; j = i; while (j>0 && temp < arr[j-1]) { //从有序序列最后i-1开始,j是插入位置 arr[j] = arr[j-1]; j--; } arr[j]=temp; }
希尔排序Shell
-
描述:
- 相当于对不同的间隔的元素序列进行排序,具体进行排序的算法可以为插入排序。
- 每一个间隔从gap开始,相当于插入排序从1开始。遍历一遍是对不同分组交替插入。
-
实现:
int temp; int j; //gap是间隔(矩阵宽度),也可以作为输入的其他值。 for (int gap = (int) Math.floor(arr.length/2); gap > 0; gap= (int) Math.floor(gap/2)) { //从gap开始(矩阵中这一列的第二个)开始向后扫描。 // 对间隔为gap的序列进行插入排序。事实上每次+1前后进行的是不同分组的排序。 for (int i = gap; i < arr.length; i++) { j = i; //j是插入位置 temp=arr[i]; while (j-gap>=0 && temp < arr[j-gap]){ arr[j] = arr[j-gap]; j-=gap; } arr[j] = temp; } }
归并排序Merge
-
描述:
- 单个元素自然有序,将两个有序序列合并为一个有序序列。
- 进行归并时,可以只复制前半部分的数组,后半部分使用原来的数组空间。
-
实现:
static void mergeSort(int[] arr, int lo, int hi) { if (hi - lo == 0) { return; } int mid = (lo + hi) / 2; mergeSort(arr, lo, mid); mergeSort(arr, mid+1, hi); merge(arr, lo, mid, hi); } static void merge(int[] arr,int lo, int mid, int hi) { int[] temp = new int[mid-lo+1]; //只复制数组的前半部分 for (int i=lo; i<=mid; i++) { temp[i-lo] = arr[i]; } int i=0; int j=mid+1; int k=lo; while (i<=mid-lo && j<=hi) { if (temp[i]<arr[j]){ arr[k++]=temp[i++]; } else { arr[k++]=arr[j++]; } } if (j>hi) { //如果是前半部分先排列完毕,则后半部分自然有序 while (i<=mid-lo) { arr[k++]=temp[i++]; } } }
快速排序Quick
-
描述:
- 用一个轴点将序列分为两部分,左侧的都比轴点小,右侧的都比轴点大。
- mid指向小于轴点分区中的最后一个元素,所以插入前需要+1。k指向当前扫描元素。
- 在不同的算法中,hi可能有不同的含义(末元素或尾哨兵),看边界是否-1,在这里是尾哨兵。
-
实现:
static void quickSort(int[] arr, int lo, int hi) { if (hi - lo <= 1) { //这里的hi是末元素的下一个,也就是结尾哨兵 return; } int mid = partition(arr, lo, hi); quickSort(arr, lo, mid); quickSort(arr, mid+1, hi); } static int partition(int[] arr,int lo, int hi) { int mid = new Random().nextInt(hi-lo) + lo; //随机选取轴点 swap(arr, lo, mid); mid = lo; for (int k = lo+1; k <hi ; k++) { if (arr[k] < arr[lo]) { swap(arr, ++mid, k); } } swap(arr, lo, mid); return mid; } static void swap(int[] arr, int a, int b) { int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; }
堆排序Heap
-
描述:
- 使用对叶子节点自下而上的下滤快速建堆。
- 对于向量组织的堆,父节点秩为i,则子节点秩为2i+1和2i+2。
- 每次取出栈顶元素后,将其放在有序序列的最前。同时维护堆序性。
-
实现:
static void heapSort(int[] arr, int lo, int hi) { buildHeap(arr, lo, hi); for (int i = hi -1; i>lo; i--) { swap(arr, lo, i); percolateDown(arr, lo, lo, i); //取出堆顶元素 } } static void buildHeap(int[] arr, int lo, int hi) { //快速建堆 for (int i = (int) Math.floor((hi-lo)/2); i >=0; i--) { //从非叶子节点开始自下而上的下滤 percolateDown(arr, i, lo, hi); } } static void percolateDown(int[] arr, int parent, int lo, int hi) { //下滤 int left = lo + (parent-lo) * 2 + 1; int right = lo + (parent-lo+1) * 2; int choice = parent; if (left < hi && arr[left] > arr[choice]) { choice = left; } if (right < hi && arr[right] > arr[choice]) { choice = right; } if (choice != parent) { swap(arr, choice, parent); percolateDown(arr, choice, lo, hi); //如果更新了,继续考察下滤后的节点 } } static void swap(int[] arr, int a, int b) { int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; }
计数排序Counting
-
描述:
- 将输入的数值存储在新的数组空间中。索引为数值的大小,值为该数值出现的次数。
- 在排序前需要知道数组中数值的大小范围。
- 映射完成后,再反向填充原数组。
-
实现:
int[] count = new int[maxNum-minNum+1]; //需要知道数组的数值范围 for (int i = 0; i < arr.length; i++) { count[arr[i]-minNum]++; //计数 } int j = 0; for (int i = minNum; i <= maxNum; i++) { while (count[i-minNum]-- > 0) arr[j++] = i; //反向填充 }
桶排序Bucket
-
描述:
- 桶排序是计数排序的升级版。不简单使用数值而是使用一个映射函数生成索引。
- 在每个索引的空间称为一个桶,在一个桶中再进行排序。
- 最后把不是空的桶中的数据拼接起来。
-
实现:
int bucketSize = 5; //每个桶中存储的范围 int bucketCount = (int) Math.floor((maxNum-minNum)/bucketSize)+1; //桶的个数,也可以用其他映射函数,保证大小次序不变即可 LinkedList<Integer>[] bucket = new LinkedList[bucketCount]; int index; for (int i = 0; i < arr.length; i++) { index = (int) Math.floor((arr[i]-minNum)/bucketSize); //装入桶中 if (bucket[index]==null) { bucket[index] = new LinkedList<>(); } bucket[index].add(arr[i]); } int j = 0; for (int i = 0; i < bucketCount; i++) { if (bucket[i]!=null){ insertSort(bucket[i]); //桶中元素排序 for (Integer ele : bucket[i]) { //输出有序序列 arr[j++] = ele; } } }
基数排序Radix
-
描述:
- 先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
- 对整数排序可按从低往高位上的数字大小作为优先级。可以取除以其他数,能覆盖元素范围即可。
- 对于每个桶,添加元素与取出元素的位置应该相反。如从尾部添加,就从头部取出,不然会破坏顺序。
-
实现:
int dev = 1; int mul = 10; //所要除的是哪一位;进制数。这里取某一位上的大小为优先级 int maxpriority = 2; //这里取十进制的个位和十位,选取时能覆盖数组中的元素即可 int bucketCount = mul; //桶的个数 LinkedList<Integer>[] bucket = new LinkedList[bucketCount]; int index; for (int i=0; i<maxpriority; dev*=mul,i++){ //每个优先级遍历一遍 for (int j = 0; j < arr.length; j++) { index = (arr[j] % (dev*mul))/dev; //取余得到优先级 if (bucket[index]==null){ bucket[index] = new LinkedList<>(); } bucket[index].add(arr[j]); } int k=0; for (int j = 0; j < bucket.length; j++) { //计数排序 if (bucket[j]!=null) { while (!bucket[j].isEmpty()) { arr[k++] = bucket[j].pop(); //注意这里与上边添加元素的位置相反 } } } }
iwehdio的博客园:https://www.cnblogs.com/iwehdio/