数据结构与算法(三)——列表
iwehdio的博客园:https://www.cnblogs.com/iwehdio/
Github:https://github.com/iwehdio/DSA_THU_DJH_asJava
导图
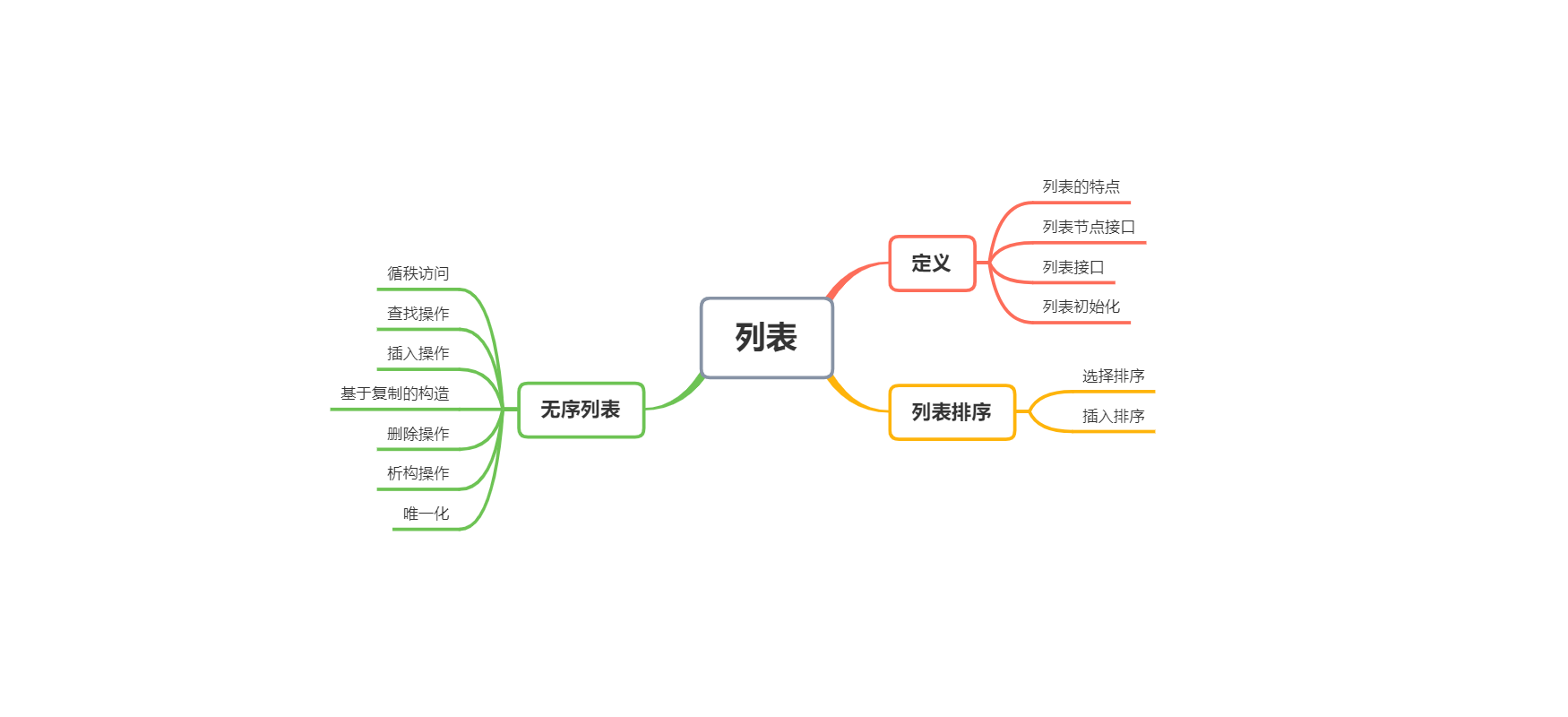
列表的Java实现见:https://www.cnblogs.com/iwehdio/p/12621460.html
1、列表的定义
-
静态与动态:
- 操作的静态与动态:
- 静态:仅读取,数据结构的内容与组成一般不变。
- 动态:需写入,数据结构的局部或整体将改变。
- 数据元素存储与组织方式的静态与动态:
- 静态:数据空间整体创建或销毁,数据元素的物理存储词语与其逻辑次序一致。 静态操作高效,动态操作相对低效。如向量。
- 动态:为各数据元素单独分配和回收物理空间。逻辑上相邻的元素记录彼此的物理地址,在逻辑上形成一个整体。动态操作高效,静态操作相对低效。如列表。
- 操作的静态与动态:
-
列表:采用动态存储的典型结构。
- 每个元素称为节点( node )。
- 各个节点通过指针或引用彼此联接,在逻辑上构成一个线性序列。
- 相邻节点彼此互称前驱和后继。如果存在前驱和后继,那么必然是唯一的。
- 没有前驱的节点称为首,没有后继的节点称为末。此外,可以认为头存在一个哨兵前驱称为头,末存在一个哨兵后继称为尾。
- 可以认为 头、首、末、尾 节点的秩分别为 -1、0、n-1、n。
- 在访问时尽量不使用循秩访问,而使用循位置访问。即利用节点之间的相互引用,找到特定的节点。
-
列表元素的ADT接口:

-
列表节点:ListNode 模板类。
#define Posi(T) ListNode<T>* //定义指向列表节点的数据类型(节点位置) template <typename T> struct ListNode{ T data; //数值内容 Posi(T) pred; //前驱 Post(T) succ; //后继 ListNode() {} //针对头尾哨兵的无参构造 ListNode(T e, Posi(T) p=null, Posi(T) s=null) : data(e), pred(p), succ(s) {} //默认构造器 Posi(T) insertAsPred(T const& e); //前插入 Posi(T) insertAsSucc(T const& e); //后插入 } -
列表的ADT接口:

-
列表:List 模板类:
#include "ListNode.h" //引入列表节点类 template <typename T> class List { private: int _size; Posi(T) header; Posi(T) trailer; //头尾哨兵 protected: /*内部函数*/ public: /*构造函数、析构函数、对外的接口函数等*/ } -
列表的初始化函数:
template <typename T> void List<T>::init() { header = new ListNode<T>; //创建头尾哨兵节点 trailer = new ListNode<T>; header -> succ = trailer; //互联元素 header -> pred = null; trailer -> pred = header; trailer -> succ = null; _size = 0; //记录规模 }
2、无序列表的操作
-
循秩访问:
-
列表也可以模仿向量的循秩访问(通过重载下标运算符)。
-
但是效率比较低,时间复杂度为 O(n) 。
-
实现:
template <typename T> T List<T>::operator[](Rank r) const { Posi(T) p = first(); //从首节点出发 while(0 < r++) p = p->succ; //顺数第r个节点 return p ->data; }
-
-
查找操作:
-
定义:在指定节点 p (可能为尾哨兵)的 n 个真前驱中找到等于 e 的最后者。
-
实现:
template <typename T> Posi(T) List<T>::find(T const& e, int n, Posi(T) p) const { while(0 < n--) //从右到左逐个比较,直到命中或越界 if(e == (p = p->pred)->data) return p; return null; }
-
-
插入操作(以前插入为例):
-
创建一个新节点 e ,并将其作为 p 的前驱插入。
-
创建新节点e,前驱是 p 的原前驱,后继是 e。设 p 的原前驱的后继是 e,p 的新前驱是 e。
-
实现:
template <typename T> Posi(T) List<T>::insertBefore(Posi(T) p, T const& e){ _size++; return p->insertAsPred(e); //把e当作p的前驱插入 } template <typename T> Posi(T) ListNode<T>::insertAsPred(T const& e){ Posi(T) x = new ListNode(e, pred, this); //创建新节点e,前驱是p的原前驱,后继是e pred->succ = x; //p的原前驱的后继是e pred = x; //p的新前驱是e return x; //返回新节点的位置 }
-
-
基于复制的构造:
-
创建一个空列表,然后将传入的自 p 节点开始的 n 项依此作为末节点插入。
-
实现:
template <typename T> void List<T>::copyNodes(Post(T) p, int n){ init(); //初始化空列表 while(n--){ //insertAsLast(p->data)实际上就是insertBefore(trailer, p->data) insertAsLast(p->data); p = p->succ; } }
-
-
删除操作:
-
传入所要删除的 p 处的节点。
-
将 p 的前驱的新后继赋值为 p 的原后继,将 p 的后继的新前驱赋值为 p 的原前驱。
-
实现:
template <typename T> T List<T>::remove(Posi(T) p){ T e = p->data; p->pred->succ = p->succ; //将p的前驱的新后继赋值为p的原后继 p->succ->pred = p->pred; //将p的后继的新前驱赋值为p的原前驱。 delete p; _size--; return e; //返回被删除的值 }
-
-
析构操作:
-
首先删除所有可见节点,然后删除头尾哨兵。
-
删除可见节点通过反复删除首节点直到规模为 0 实现。
-
实现:
template <typename T> List<T>::~List() //列表析构 { clear(); delete header; delete trailer; } template <typename T> int List<T>::clear(){ int oldSize = _size; while(0 < _size){ remove(header->succ); } return oldSize; }
-
-
列表的唯一化:
-
删除无序列表中的重复节点。
-
从首节点开始,依此寻找其前驱中是否有重复节点。使得向后扩展时,搜索节点的前驱总是无重复的,这样就只需比对该搜索节点在前驱中是否有雷同项。
-
实现:
template <typename T> int List<T>::dedupicate(){ if(_size < 2) return 0; int oldSize = _size; Posi(T) o = first(); //从首节点开始 Rank r = 1; while(trailer != (p = p->succ)){ Posi(T) q = find(p->data, r, p); //在p的r个真前驱中,有没有雷同的 q ? remove(q) : r++; //如果有雷同的就移除前驱中雷同的项,否则将不雷同的前驱向后扩展一项 } return oldSize - _size; //返回被删除的元素数 }
-
-
有序列表的唯一化:
-
删除有序列表中的重复节点。
-
由于有序,如有雷同则必定是紧邻在一个区段中的。
-
p 指向每个区段的第一个节点,删除与之相同的后继。如果出现不相同的后继,则 p 指向这个后继。
-
实现:
template <typename T> int List<T>::uniquify(){ if(_size < 2) return 0; int oldSize = _size; ListNodePosi(T) p = first(); //p初始化为首节点,p为每个区段的首节点 ListNodePosi(T) q = p->succ; //q为各个区段中p的后继 while(trailer != (q->succ)){ //考察紧邻的节点对 if(p->data != q->data){ p = q; } else { remove(q); } q = p->succ; } return oldSize - _size; } -
时间复杂度为 O(n)。
-
-
有序列表查找操作:
- 与无序向量的查找算法完全相同,在效率上并没有提高,这是由列表的循位置访问的特点决定的。
3、选择排序与插入排序
-
选择排序:
-
选取所有元素中最大的放在列表末,然后再选择剩下的元素中最大的放在末的前驱位置,反复执行。也就是说,每次选择出剩余集合中的最大值。
-
冒泡排序就是一种选择排序,但是由于每次只进行相邻元素的位置交换,导致效率很低。
-
改进思路:将序列分为前缀无序子序列 U 和后缀有序子序列 L ,其中 L 中的元素大于等于 U 中的元素。在每次迭代中,选取 U 中最大的元素,并将其移动至 L 的最前端。
-
实现:
template <typename T> void List<T>::selectionSort(Posi(T) p, int n){ Posi(T) head = p->pred; Posi(T) tail = p; for(int i=0; i<n; i++) tail = tail->succ; //待排序区间为(head,tail) //从待排序区间内找出最大者,将其从原位置删除并插入tail的位置,然后将tail前移,,待排序区间宽度-1 while(1 < n){ //insertBefore()和remove()虽然可以认为时O(1)时间,但由于使用了动态内存分配,会使效率大大降低。实际上更倾向于进行节点数据域的交换 insertBefore(tail, remove(selectMax(head->succ, n))); tail = tail->pred; n--; } } template <typename T> //获取起始于p的n个元素的最大值,画家算法 Posi(T) List<T>::selectMax(Posi(T) p, int n){ Posi(T) max = p; //初始化p为最大 for(Posi(T) cur=p; 1<n; n--){ //后续节点与max逐一比较,!lt(a,b)比较器表示a不小于(not less than,即>=)b时 if(!lt((cur=cur->succ)->data, max->data){ max = cur; } } return max; } -
时间复杂度总是 Θ(n^2),没有最好和最坏情况。但是与冒泡排序相比元素移动操作大大减少。
-
-
插入排序:
-
将整个序列分为前缀有序序列 [ 0, r ) 和后缀无序序列 [ r, n),然后将第 r 个元素插入到前缀有序序列中的合适位置,使得前缀有序序列仍然有序并且规模加一。
-
与选择排序的区别:选择排序中无序部分中元素总小于有序部分,而插入排序无此限制;而且因此选择排序的操作对象为无序部分中的最大值,而插入排序的操作对象为无序部分与有序部分交界的元素。
-
实现:
template <typename T> void List<T>::insertionSort(Posi(T) p, int n){ for(int r=0; r<n; r++){ //r实际上就是有序前缀序列的长度 //每次在search()返回的位置插入,然后删除原位置上的节点 insertAfter(search(p->data, r, p), p->data); p = p->succ; remove(p->pred); } } -
时间复杂度:最好 O(n),最差 O(n^2),平均复杂度为 O(n^2)。
-
逆序对:两个元素前大后小。
- 如果 a、b 是一个逆序对( a>b ),我们将 b 所对应的逆序对数加一。也就是某个元素对应逆序对数,记为其作为逆序对中较右、较小的角色的逆序对数量。
- 对于插入排序,列表的逆序对数就表征了所要进行的比较次数。最好情况下,列表为顺序的,逆序对数为 0 。最差情况下,列表为逆序的,逆序对数为 n^2。时间复杂度为插入时间加比较时间,比较时间最好为 0,最差为 O(n^2);插入时间为 O(n)。则总得复杂度为最好 O(n),最差 O(n^2)。
- 插入排序的时间复杂对依赖于输入序列的逆序对数,是输入敏感的。
-
参考:数据结构与算法(清华大学C++描述):https://www.bilibili.com/video/av49361421
iwehdio的博客园:https://www.cnblogs.com/iwehdio/