Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
2 / 1 3
Binary tree [2,1,3], return true.
Example 2:
1 / 2 3
Binary tree [1,2,3], return false.
给定一个二叉树,判断它是否是合法的二叉查找树(BST)
一棵BST定义为:
- 节点的左子树中的值要严格小于该节点的值。
- 节点的右子树中的值要严格大于该节点的值。
- 左右子树也必须是二叉查找树。
- 一个节点的树也是二叉查找树。
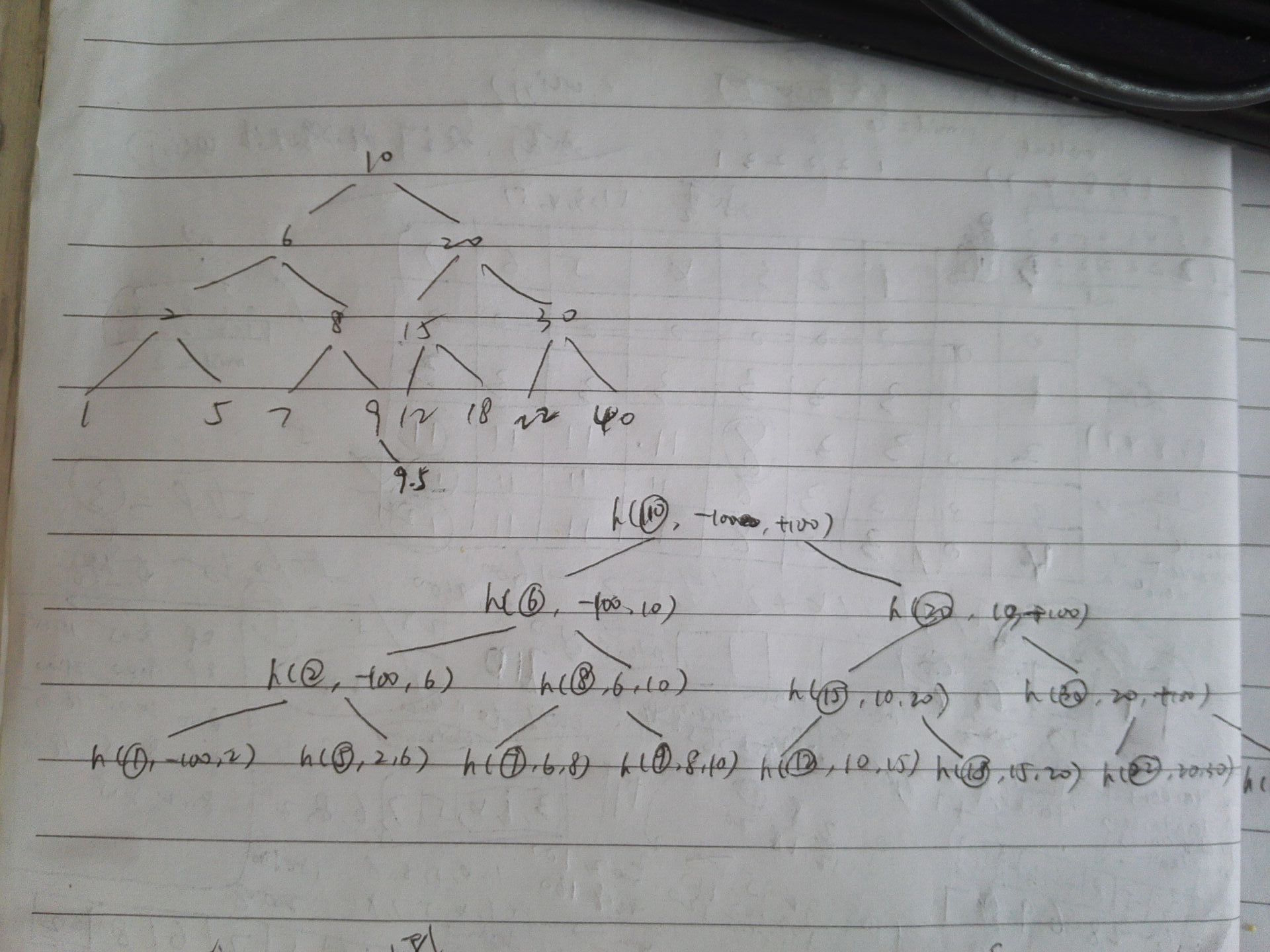
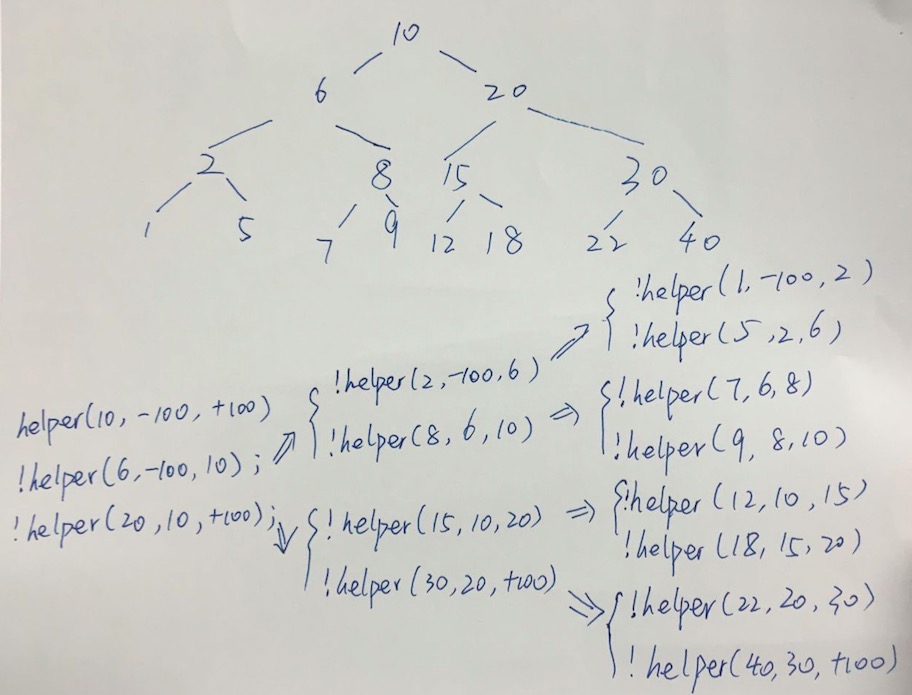
每个结点都得和两个数比,它必须在这两个数的范围之内,其中一个就是它的父节点,另外一个是它的某个祖先借点
这个树是从上往下遍历的,遍历到每个节点时,都要把它限定在一个已知的范围内,不管他下面的节点,只根据他上面的节点来找出这个范围
20
/
15
/
12
/
5
7
9
11
7 9 11就都得和他们自己的父节点比, 另外都和12比 因为他们都在12的左子树中,所以都应该比12小
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class Solution { public boolean isValidBST(TreeNode root) { if (root == null) { return true; } return helper(root, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY); } public boolean helper(TreeNode root, double low, double high) { if (root.val <= low || root.val >= high) { return false; } if (root.left != null && !helper(root.left, low, root.val)) { return false; } if (root.right != null && !helper(root.right, root.val, high)) { return false; } return true; } }