1、数据质量分析
脏数据:缺失值、异常值、不一致的值、重复数据及含有特殊符号的数据
缺失值处理
产生原因
1、信息无法获取或者获取代价大
2、信息因个人原因或客观原因被遗漏
3、根据实际而言,属性值不存在
影响
1、丢失大量有用信息
2、不确定性更加显著,难以把握规律
3、不可靠输出
分析
1、含有缺失值的属性的个数
2、每个属性的未缺失数、缺失数、缺失率
处理
1、删除存在缺失值的记录
2、对可能值进行插补
1)均值/中位数/众数插补
2)使用某个常数插补
3)最近邻插补,采用距缺失样本最近的样本值。
4)回归拟合,预测缺失的属性值
5)插值法,利用已知点建立插值函数,缺失值由插值函数对应点上的值近似代替。
3、不处理
异常值处理
异常值是指样本中的个别值,数值明显偏离其余的观测值,也称离群点。
分析
1、描述性统计,比如最大值、最小值,看那些数据取值超出合理范围
2、3σ原则
当数据服从正态分布,在该原则下,异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。在正态分布的假设下,数据位于距平均值超过3σ的概率为  ,属于小概率事件。
,属于小概率事件。
3、箱型图(箱线图)分析
异常值被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。QL为下四分位数,表示有四分之一的数比其小;QU为上四分位数,表示全部数据中有四分之一的数值比其大;IQR为四分位数间距,IQR=QU-QL。
处理
1、删除含有异常值的记录
2、视为缺失值进行处理
3、采用前后两个观测值的平均值修正
4、不处理
一致性处理
数据不一致性是指数据的矛盾性、不相容性。
导致数据不一致通常在数据集成的过程中,对不同的数据源的重复存放的数据未能进行一致性更新导致的。
2、数据特征分析
1、分布分析
定量数据
主要采用频率分布直方图。
1、求极差
2、决定组距与组数
3、决定分点
4、列出频率分布表,绘制频率分布直方图
定性数据
常采用饼图或条形图描述。
2、对比分析
1、绝对数比较
2、相对数比较
是由两个有联系的指标对比计算的。
1、结构相对数:部分数值占总体数值的比重,比如食品支出占消费总额比重、产品合格率
2、比例相对数:部分之间对比,如人口性别比例,投资与消费比例
3、比较相对数:同一时期两个性质相同的指标进行对比,说明同类现象在不同空间条件下的数量对比。如不同地区商品价格对比等..
4、强度相对数:将两个性质不同但有一定联系的总量指标对比,说明现象的强度、密度、普遍程度等。如人均国内生产总值、人口密度、人口出生率。
5、计划完成程度相对数:某一时期实际完成数与计划数的对比。
6、动态相对数:同一现象在不同时期的指标数值进行对比,说明发展方向和变化速度。
3、统计量分析
1、集中趋势
1)均值
平均值:
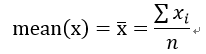
加权平均:
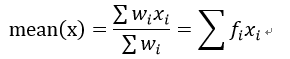
截断均值:去掉高、低极端值之后的平均值。
2)中位数
3)众数
2、离中趋势
1)极差
极差=最大值-最小值
2)标准差
标准差度量数据偏离均值的程度:
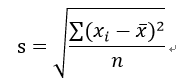
3)变异系数
变异系数度量标准差相对于均值的离中趋势:

4)四分位数间距:
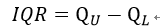
4、周期性分析
常通过绘制曲线图来分析
5、贡献度分析
贡献度分析又称帕累托分析,原理为帕累托法则,有成20/80定律。例如,对一个公司而言,80%的利润常常来自于20%最畅销的商品,而其他80%的商品只产生20%的利润。
常通过绘制帕累托图分析。
6、相关性分析
1、绘制两个变量的散点图
2、多变量时,绘制散点图矩阵。
3、计算相关系数
1)Pearson相关系数
一般用于分析两个连续性变量之间的关系,要求连续变量取值服从正态分布:

r的取值范围为:-1≤r≤1:

需要进行假设检验,可采用t检验方法检验显著性水平以确定相关程度。
2)Spearman秩相关系数
也称为等级相关系数:

先对x、y分别从小到大排序,求xi、yi的秩次Ri、Qi 。注意一个变量相同取值要有相同的秩次。

当两个变量具有严格单调的函数关系,则一定完全Spearman相关。
需要进行假设检验,可采用t检验方法检验显著性水平以确定相关程度。
3)判定系数
判定系数为相关系数的平方,用 表示。用以衡量回归方程对y的解释程度。 越接近1,表明x与y之间的相关性越强。
3、数据集成
1、实体识别
主要任务是统一不同源数据的矛盾。
1)同名异义
数据源A中的属性ID和数据源B中的属性ID分别描述的是菜品编号和订单编号,即描述的是不同的实体。
2)异名同义
A.sales_dt=B.sales_date。
3)单位不统一
比如分别用国际单位和中国传统的计量单位。
2、冗余属性识别
1)同一属性多次出现。
2)同一属性命名不一致导致重复。