原文地址:https://www.geeksforgeeks.org/insertion-in-a-binary-tree-in-level-order/
给定一个二叉树和一个数据,按层次寻找第一个可用的位置将数据插入二叉树中
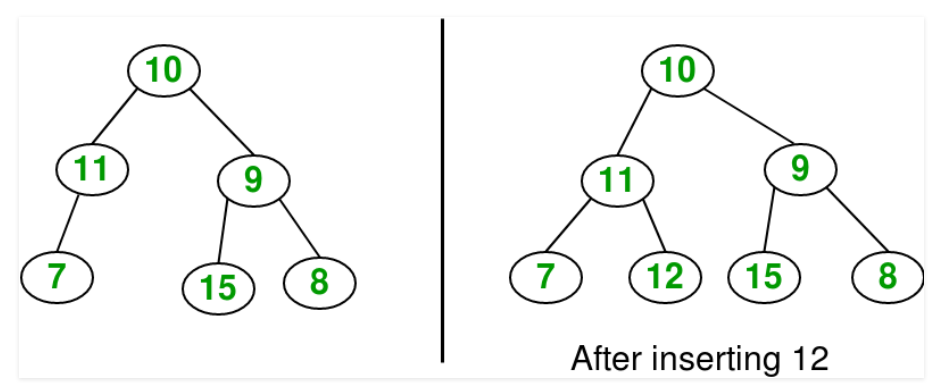
在遍历的过程中,如果我们发现一个节点的左节点是空的,我们可以用给定的数据new一个节点插入左子节点。对于右子节点同理。
package bst;
import java.util.LinkedList;
import java.util.Queue;
public class GFG {
//一个树节点有三个关键点:左子树指针,右子树指针,数据部分,
//这里我们用int作为数据部分,实际应用中key的数据类型可以是任意的数据类型
static class Node {
int key;
Node left, right;
Node(int key){
this.key = key;
left = null;
right = null;
}
}
static Node root;
static Node temp = root;
//在遍历二叉树的时候分为两大类,一种是BFS(广度优先遍历)即Breadth FirstSearch
//一种是DFS(深度优先遍历)即Depth First Search,深度优先遍历又分为前序,中序和后序。
static void inorder(Node temp)
{
if (temp == null)
return;
inorder(temp.left);
System.out.print(temp.key+" ");
inorder(temp.right);
}
//插入节点
static void insert(Node temp, int key)
{
Queue<Node> q = new LinkedList<Node>();
q.add(temp);
// 层次遍历,直到寻找到一个可用的位置插入节点
while (!q.isEmpty()) {
temp = q.peek();
q.remove();
if (temp.left == null) {
temp.left = new Node(key);
break;
} else
q.add(temp.left);
if (temp.right == null) {
temp.right = new Node(key);
break;
} else
q.add(temp.right);
}
}
public static void main(String args[])
{
root = new Node(10);
root.left = new Node(11);
root.left.left = new Node(7);
root.right = new Node(9);
root.right.left = new Node(15);
root.right.right = new Node(8);
System.out.print( "Inorder traversal before insertion:");
inorder(root);
int key = 12;
insert(root, key);
System.out.print("
Inorder traversal after insertion:");
inorder(root);
}
}