目录
摘要
围棋的困难点分析
如何绕过困难点
AlphaGo思想简介
网络训练流程分析
1.策略网络的监督学习
2.策略网络的强化学习
3.价值网络的强化学习
4.策略网络、价值网络联合MCTS
AlphaGo算法小结
AlphaGo棋力评估
Discussion
AlphaGo中MCTS的细节*
参考资料
|
摘要 |
用AI下围棋是一个非常大的挑战，因为围棋具有巨大的搜索空间，也难以评估棋面和动作的好坏。DeepMind提出了一种新的方法，即使用价值网络(value networks)来评估棋面好坏，使用策略网络(policy networks)来选择落子动作。这两个网络的训练过程有一些创新，使用的训练数据有人类高手的对弈数据以及AI左右博弈的数据。单纯的使用这两个网络，就可以达到蒙特卡洛树搜索（MCTS，以前的下棋程序主要用它）的水平。Deepmind又进行了创新，即把这两者（两个网络、MCTS）有机合并，最终达到了非常好的效果（打败欧洲冠军樊麾）。
|
围棋的困难点分析 |
具有完备信息的游戏都会有一个最优的价值函数(value function)，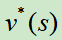
，它能够在任何的状态s（棋面）下知道游戏的最终胜负。其实就是穷举的思想，做法就是在某个状态下，递归的向下展开游戏树，然后就知道所有落子位置的精确胜率。但是，展开一棵游戏树是不可能的，因为复杂度太高为
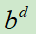，b表示游戏的宽度（可以落子的位置数），d是深度（游戏的长度）。
|
如何绕过困难点 |
所以就需要对价值函数进行近似，可以从两方面入手：
1.减少搜索深度：
通过位置评估的方式，对树的搜索进行截断。比如搜索到某个状态s，使用一个近似函数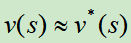
来预测当前价值，就不继续向下展开游戏树了。
2.减少搜索宽度：
在某个状态下，不对所有的可以落子的位置进行搜索，而是通过落子位置采样的方式，也就减小了搜索宽度。落子的采样可以服从策略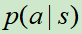
的分布。
|
AlphaGo思想简介 |
使用残差网络的架构，将棋盘状态编码为19*19的张量（19是棋盘大小）作为输入，来训练价值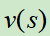网络
和策略网络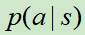
。
网络的训练分成了几个阶段：
1.训练监督学习策略（SL）网络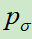
，使用的是人类围棋专家的对弈数据。使用相同的方法，再训练监督学习策略网络
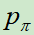，该网络更小，推理速度更快。
2.训练强化学习策略（RL）网络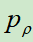
，该网络训练参数以
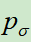的参数为起点，使用左右博弈产生的数据，进行强化学习，可以理解成对
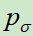的进一步提升。这里补充一下，SL模型的输出是对准确率的预测（输入一个棋面，输入下一步落子位置），而RL模型就是要突破人类的经验，去探索对取胜更有价值的路数。
3.训练一个价值网络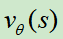
，该网络输入的是棋面，输出的是获胜的概率，其中使用的下棋策略就是RL模型。
以上就是网络训练部分
但是最终Deepmind还借鉴了MCTS的思想，对AlphaGo的能力做了进一步的提升。
|
网络训练流程分析 |
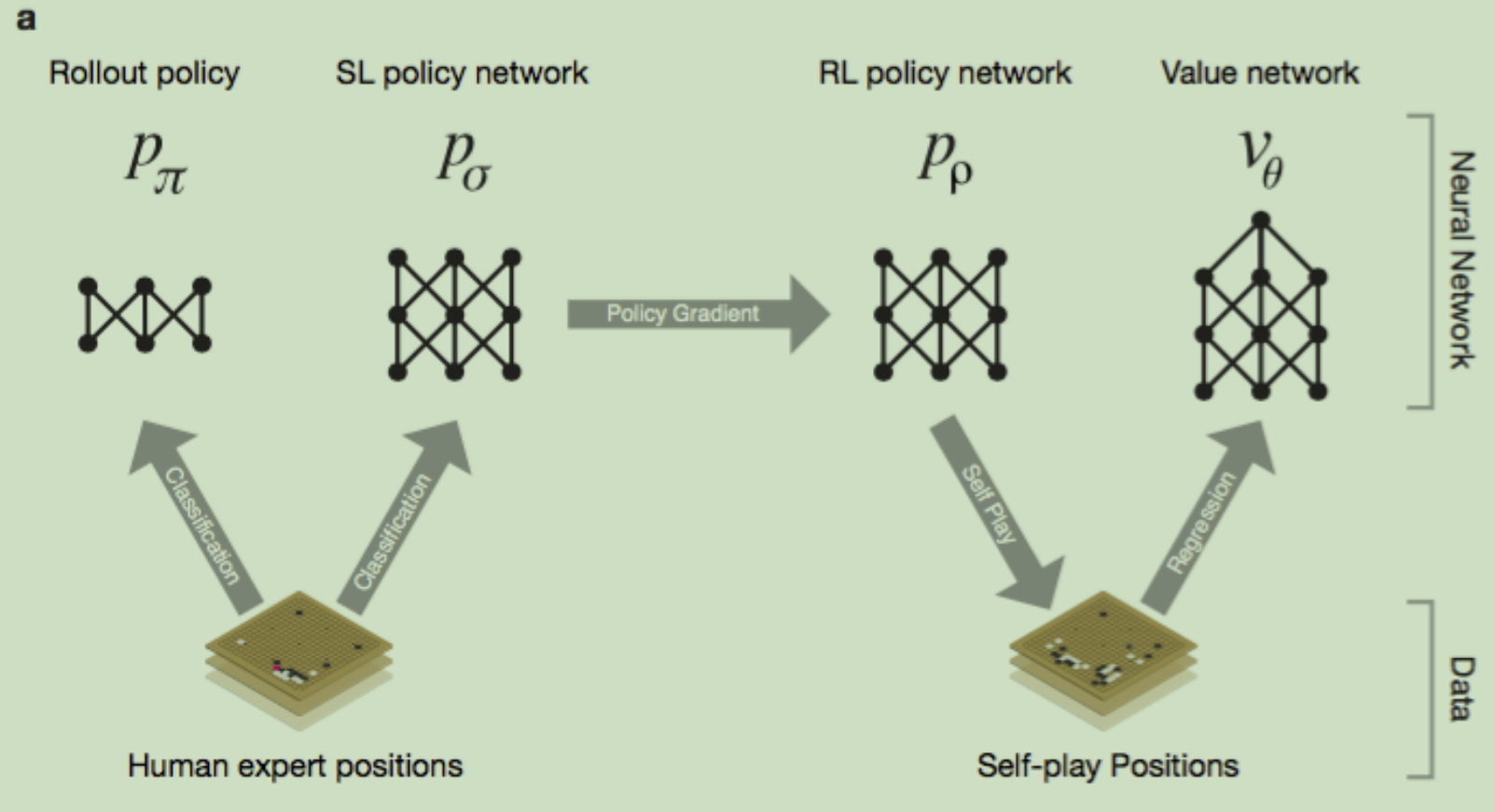
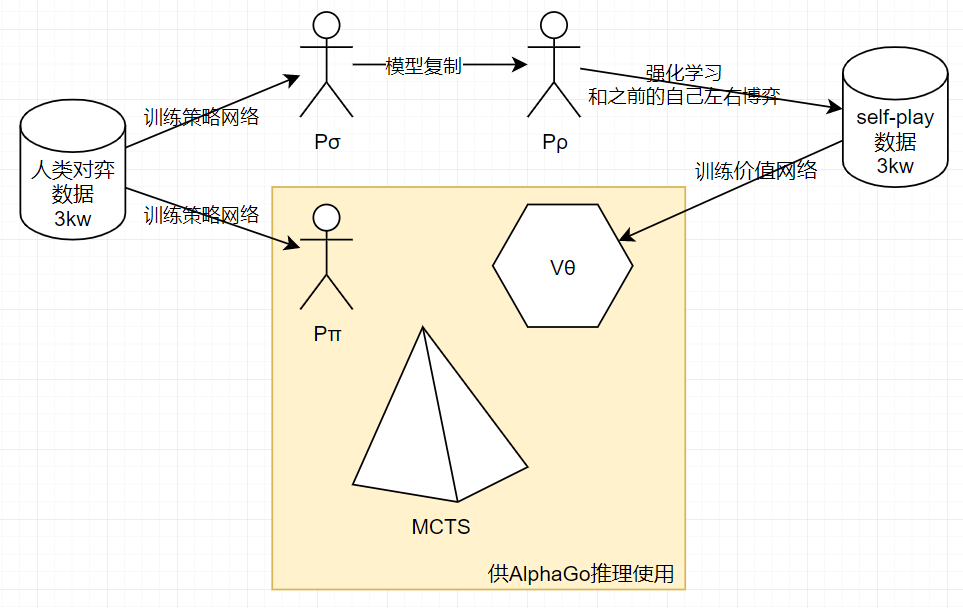
在上图a中，可以看出，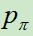
和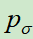
使用人类专家的下棋动作来进行监督学习训练（Softmax多分类）。
拷贝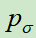
的参数，再让
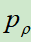左右博弈，自己和若干轮前的自己博弈，使用policy Gradient进行强化学习，得到自我对弈的数据。
使用自我对弈的数据，通过回归的方式训练价值网络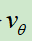
，输入是棋面，输出是该棋面的价值
在上图b中可以看出：
策略网络，输入的是棋面，输出的是合理落子位置的概率（向量）
价值网络，输入的是棋面，输出的是价值（标量）
下面对每一个细节进行展开，包括：
1.策略网络的监督学习
2.策略网络的强化学习
3.价值网络的强化学习
4.策略网络、价值网络联合MCTS
|
1.策略网络的监督学习 |
SL策略网络
的结构是卷积网络（13层），参数为σ，和relu激活函数，输出层是Softmax分布，每个值表示一个位置落子的概率。
训练数据是人类围棋高手的3kw盘对弈数据，输入是某一个棋盘状态s，标签是下一个落子动作a，参数更新为梯度上升法，梯度值为
AlphaGo Zero的棋盘状态的表示比较简单（只使用黑白，19*19*2），但是AlphaGo的棋盘状态略微复杂（如下表所示，19*19*48），
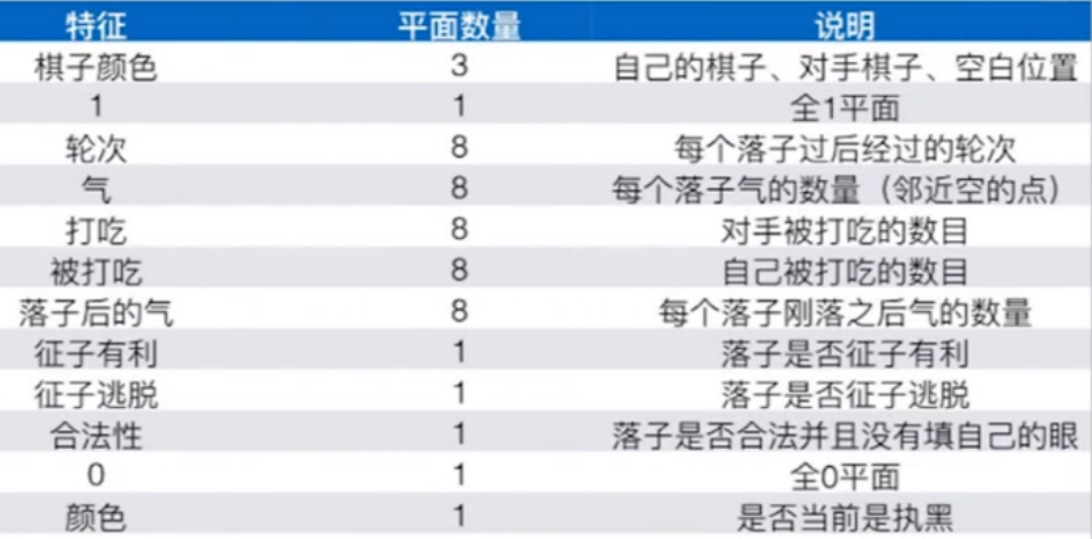
模型的训练结果是：在测试集上的准确率为57%。使用同样的方法也训练了一个小的网络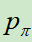
，它的准确率低（24.2%）但是推理速度快（2微妙，
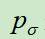是3毫秒）。
卷积核多少对结果影响的分析：
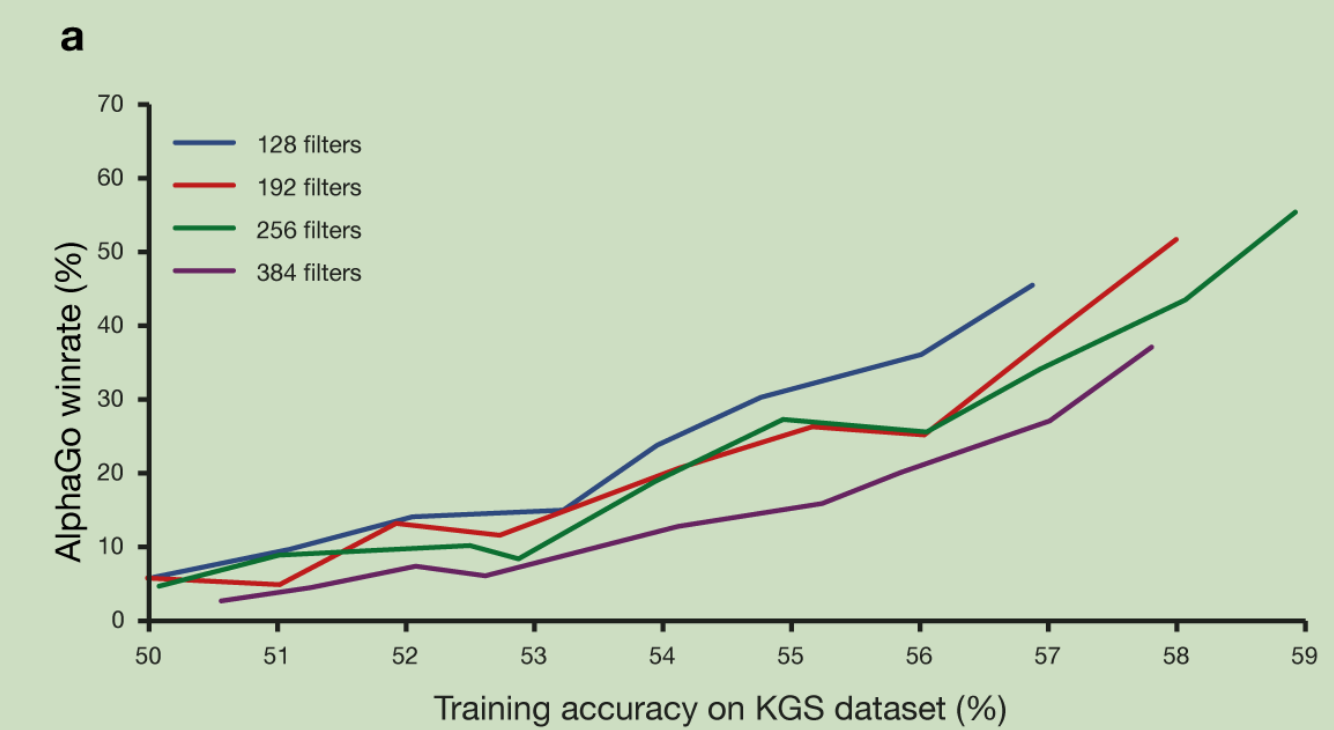
策略网络每一层的卷积核个数可以选128,192,256,384，上图描述了不同参数下，AlphaGo的胜率（最新策略和若干轮前的策略）。可以看出256的训练准确率最高，胜率也是最高。
|
2.策略网络的强化学习 |
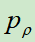使用
来初始化，即网络结构和参数都一样。使用当前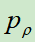
和之前轮中随机抽出的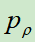进行对弈，这种随机的从对手池中选择对手的方式可以防止过拟合，使得训练更加稳定。
网络更新方法采用随机梯度下降法，梯度为：
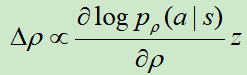
其中，如果以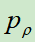取胜结束，z=1，否则为-1。其实就是赢了就加强
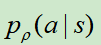，输了就降低
。
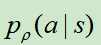RL模型的效果，和SL模型对弈可以有80%的胜率。
|
3.价值网络的强化学习 |
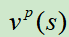计算的是在状态s下，使用策略p的价值
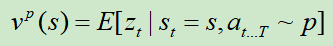
然而，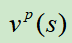
只能使用一个价值网络
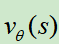来逼近，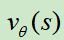
训练的输入是某一个棋面状态，标签是最终是否取胜（-1或+1），损失函数使用MSE，使用随机梯度上升更新参数，参数的梯度为
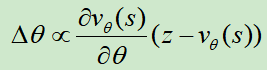
这里有一个训练的技巧，训练数据不能够按照游戏的顺序输入，因为前后的样本只有一个棋子位置的不同，这样会导致模型过拟合。Deepmind的做法是从不同的棋局（RL自我对弈）中随机抽取训练样本，最终的模型效果是MSE=0.226（训练），MSE=0.234（测试）
价值网络的真实表现如何呢？下图进行了比较
可以看出，value network的效果比MCTS+
预测得概率更准；
value network比MCTS+
预测稍差一些，但是减少了1万5千倍的计算量。
|
4.策略网络、价值网络联合MCTS |
AlphaGo将策略网络和价值网络和MCTS算法进行了结合，这样可以让AlphaGo具有向前搜索动作的特质，可以做出更佳的决策。结合的方式如下图所示：
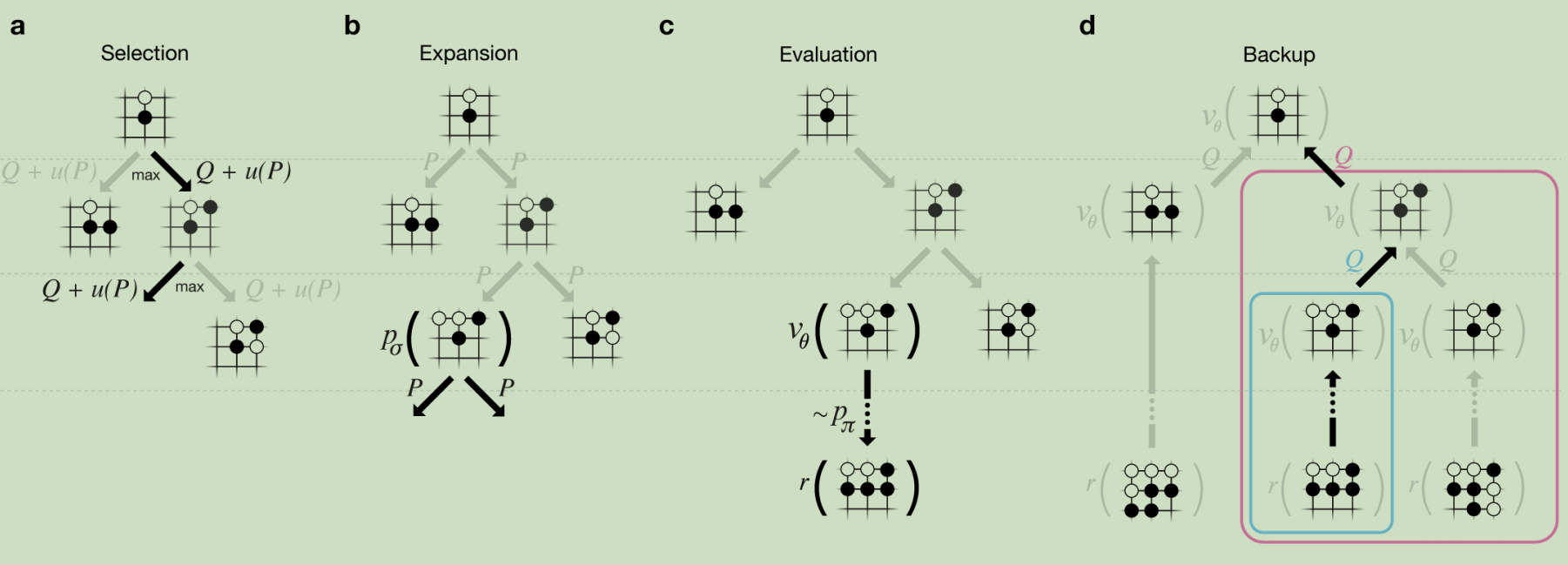
搜索树的每一条边(s,a)上，存储了一个动作价值Q(s,a)、访问次数N(s,a)和先验概率P(s,a)。
从根结点开始对该树进行仿真遍历（仿真遍历其实就是从某个位置，使用某个策略，玩到游戏结束）。在仿真过程的每一个时间步t，基于状态st选择at的方法为：
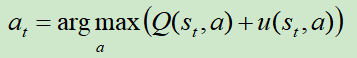
其中，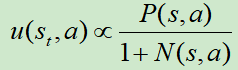
，先看分母，就是鼓励探索的机制；再看分子P(s,a)是由SL模型进行计算所得的先验概率，这里为什么不使用更强的RL模型呢？Deepmind给出的答案是，他们通过实践发现SL的效果更好，可能因为SL模型学习的是人类高手，他们会给出多种多样的走棋方式，更适宜和MCTS进行结合；而RL模型的走棋路数较为单一，会限制和MCTS结合的效果。
在研究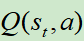
之前需要先研究
。
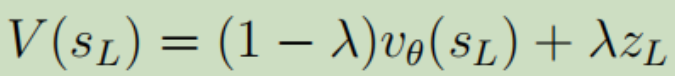
sL是当前蒙特卡洛树的叶子结点（结点就是对应某个棋面状态）；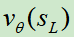
是价值网络对该状态估计出来的价值；zL是由
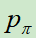在该状态下玩到游戏结束获得的回报值；λ是一个平衡因子。
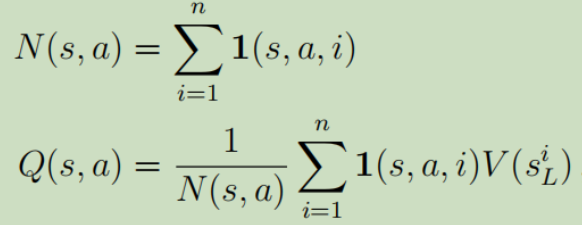
其中n表示MCTS的仿真次数。N(s,a)就是边(s,a)的总访问次数。
动作价值Q就是把(s,a)边下面子树所有的叶节点的V求均值。
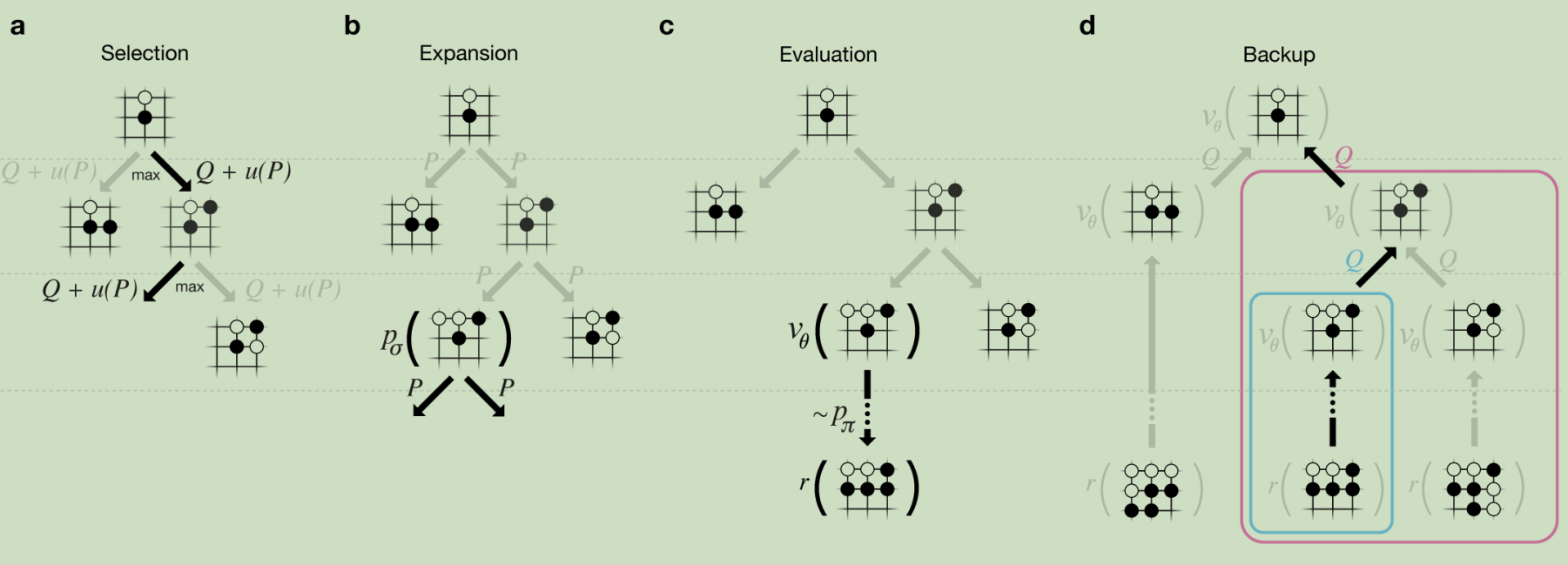
再回过头来看此图（MCTS和AlphaGo的结合），
a.每次仿真遍历树通过选择最大动作价值Q和u(P)的边。
b.叶结点可能会被扩展（依照MCTS的原理，首次遍历会求值，非首次遍历就会扩展，列出所有可能的动作），新的结点会被
计算一次，并且存为每个动作的先验概率P。
c.在仿真结束时，叶结点被两种方式评估：价值网络
和使用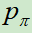
进行游戏到结束然后计算回报值r.
d.自底向上地更新(s,a)对应的动作价值Q。
Deepmind补充：如前面所说的先验概率采用的是SL模型（前面已经给出原因），但是在训练价值网络层面，经实践证明，使用RL模型产生的数据训练价值网络效果会更好。
最终模型在推理的时候，单机版AlphaGo使用了48个CPU和8个GPU，CPU开40线程进行树搜索，GPU提供网络传播的运算。分布式版本的AlphaGo使用了1202个CPU和176个GPU，并实现了分布式版本的MCTS。这里补充一点：推理时间是影响AlphaGo水平的一个关键因素，主要就是因为MCTS的采样特点，采样的越多，计算的越准，也就越耗时。
|
AlphaGo算法小结 |
|
AlphaGo棋力评估 |
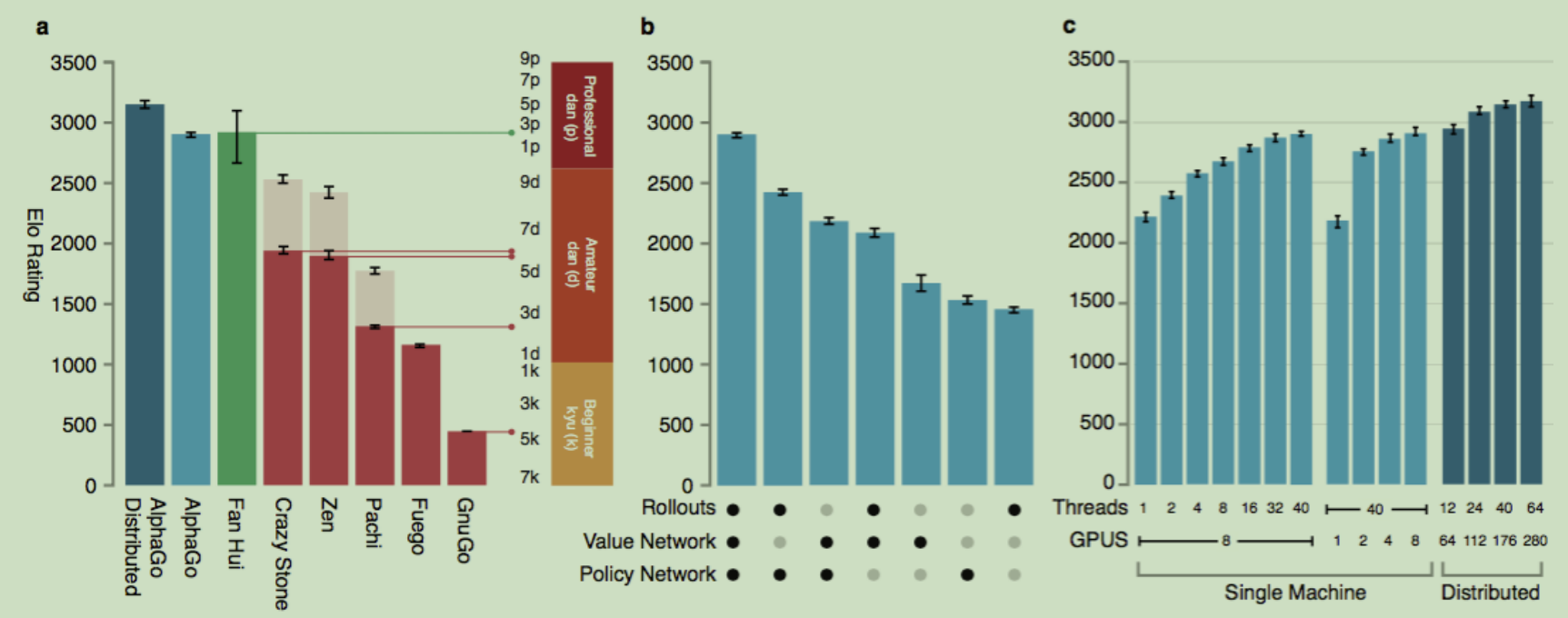
上图a中，其他的围棋程序主要以高性能的MCTS为主，限制每步计算时间为5秒，可以看出分布式版本的AlphaGo效果很好。
上图b中，可以看到综合使用这几种策略，效果更佳。
上图c说明分布式版本的优势。
|
Discussion |
Deepmind基于深度神经网络和树搜索，使用监督学习和强化学习算法，发明了围棋AI程序——ALphaGo，这是这个时代的一大壮举。AlphaGo不仅达到了围棋的专业水平，也让人们看到了AI在其他人们认为难以攻克的领域取得突破的曙光。
|
AlphaGo中MCTS的细节* |
这里对MCTS的一些细节进行解析，感兴趣的读者可以阅读。
为了让AlphaGo更高效地利用神经网络，Deepmind发明了APV-MCTS（asynchronous policy and value MCTS）。
搜索树上的每一个状态结点记为s，每一条边记为(s, a)表示每一个合法的动作，每一条边上存着一个数据集合：{P(s, a), Nv(s, a), Nr(s, a), Wv(s, a), Wr(s, a), Q(s, a)}。
P(s, a)表示该边被选中的先验概率（使用pσ算的）;
Nv(s, a)表示该边被访问的次数；
Nr(s, a)也表示该边被访问的次数，这里之所以使用两个变量，是为了使用虚拟损失，以并行化MCTS；
Wv(s, a)表示总的动作价值（total action-value），每次仿真执行这条边上的a，都会由价值网络算出一个v，就是v的累加。
Wr(s, a)表示总的rollout动作价值（total action-value），每次仿真执行这条边上的a，都会用pπ玩到游戏结束得到一个结果z，就是z的累加。
Q(s, a)表示平均动作价值（mean action-value）。
多个仿真会在不同的搜索线程中并行执行，APV-MCTS算法执行步骤如下图所示：
在上图a中，展示的是选择（Select）。每一次仿真从搜索树的根结点s0出发，在时间步L到达叶结点SL该次仿真过程结束，期间使用的策略是pπ。在每一个时间步t<L，选择动作的依据为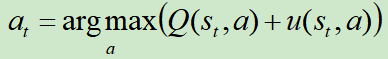
，Q还是如前文所述，但是u略有变化，这里使用了一个PUCT的变体算法，其中
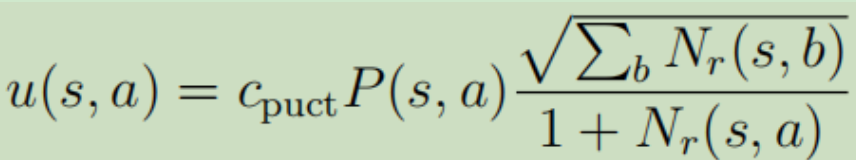，cpuct是一个控制探索的常量。
上图c中，展示的是评估（Evaluate）。叶结点SL被添加到队列，然后由价值网络进行评估。然后以该叶结点为起点进行第二次仿真，这次一直玩到游戏结束，期间使用的策略也是pπ。游戏结束后会返回一个分数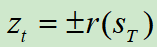
。
在上图d中，展示的是回溯（Backup）【这里难度较大，因为这里涉及到MCTS的并行化搜索】。在仿真过程中的每一个时间步t<L，在rollout过程中，其统计数据会被更新，更新的原则就是假定他输了nvl 场（论文里取nvl=3）游戏，即，Nr(st, at) = Nr(st, at) + nvl ; Wr(st, at) = Wr(st, at) - nvl；这个虚拟损失的作用就是不鼓励其他线程也同时地探索这个位置。当这次仿真结束了，就把真实的值赋值回来，即Nr(st, at) = Nr(st, at) - nvl +1; Wr(st, at) = Wr(st, at) + nvl + zt；【这里的+1表示该边被多访问了一次，+z表示把真实的游戏结果加到总的rollout动作价值】。
和价值网络有关的更新比较，即Nv(st, at) = Nv(st, at) +1; Wv(st, at) = Wv(st, at) + vθ(sL)；
至于Q，就是一个带权和，（论文中取λ=0.5）
整个的更新过程是一个无锁树的更新（lock-free）。
在上图b中，展示的是扩展（Expansion）。【这里使用了树策略，动态调整阈值等，已经被AlphaGo Zero抛弃，感兴趣的读者可以自行研究】
在所有的搜索结束后，AlphaGo会以执行访问次数最多的边上的动作，这样会对异常值更稳定，那用N的合理性在哪呢？其实换个角度想想就明白了，如果一个结点被探索的次数很多，说明该结点下的子结点一定含有很多“高招”）。落子完成后，搜索树可以被重用，被选中的边的子结点又变成根结点，上面的统计值继续使用，未被选中的分支会被舍弃。当搜索树的根结点和最好的子结点的胜率小于一定阈值（10%）时AlphaGo Zero就会认输。
|
参考资料 |
《Mastering the game of Go with deep neural networks》
MCTS可以参考：https://www.bilibili.com/video/BV1JD4y1Q7mV?from=search&seid=191148648235214401