目录
二维Full卷积
二维Same卷积
二维Valid卷积
三种卷积类型的关系
具备深度的二维卷积
具备深度的张量与多个卷积核的卷积
参考资料
二维卷积的原理和一维卷积类似,也有full卷积、same卷积和valid卷积。
举例:3*3的二维张量x和2*2的二维张量K进行卷积

|
二维Full卷积 |
Full卷积的计算过程是:K沿着x从左到右,从上到下移动,每移动到一个固定位置,对应位置的值相乘再求和,计算过程如下:

Full卷积的过程记为Cfull=x★K:

|
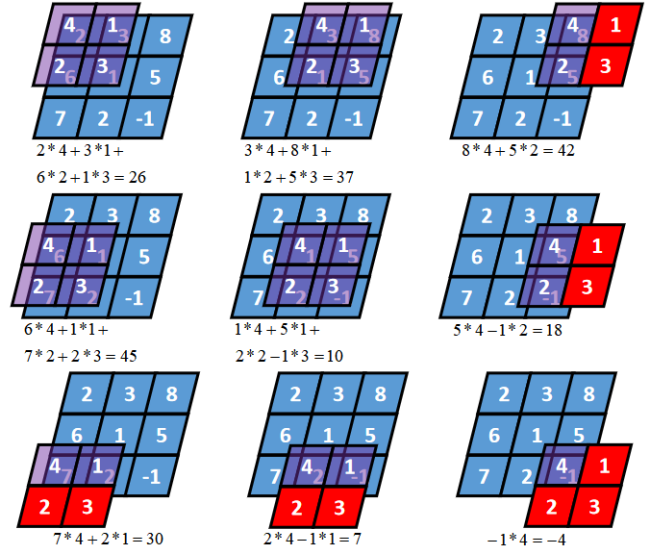
二维Same卷积 |

假设卷积核的长度为FL,如果FL为奇数,锚点位置在(FL-1)/2处;如果FL为偶数,锚点位置在(FL-2)/2处。
卷积核K都有一个锚点,然后将锚点从左到右,从上到下移动到张量x的每一个位置处,对应位置相乘再求和,计算过程如下:

|
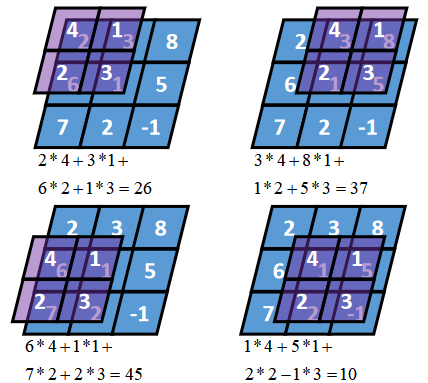
二维Valid卷积 |
从full卷积的计算过程可知,如果K靠近x,就会有部分延伸到x之外,valid卷积只考虑x能完全覆盖K的情况,即K在x的内部移动的情况,计算过程如下:

|
三种卷积类型的关系 |
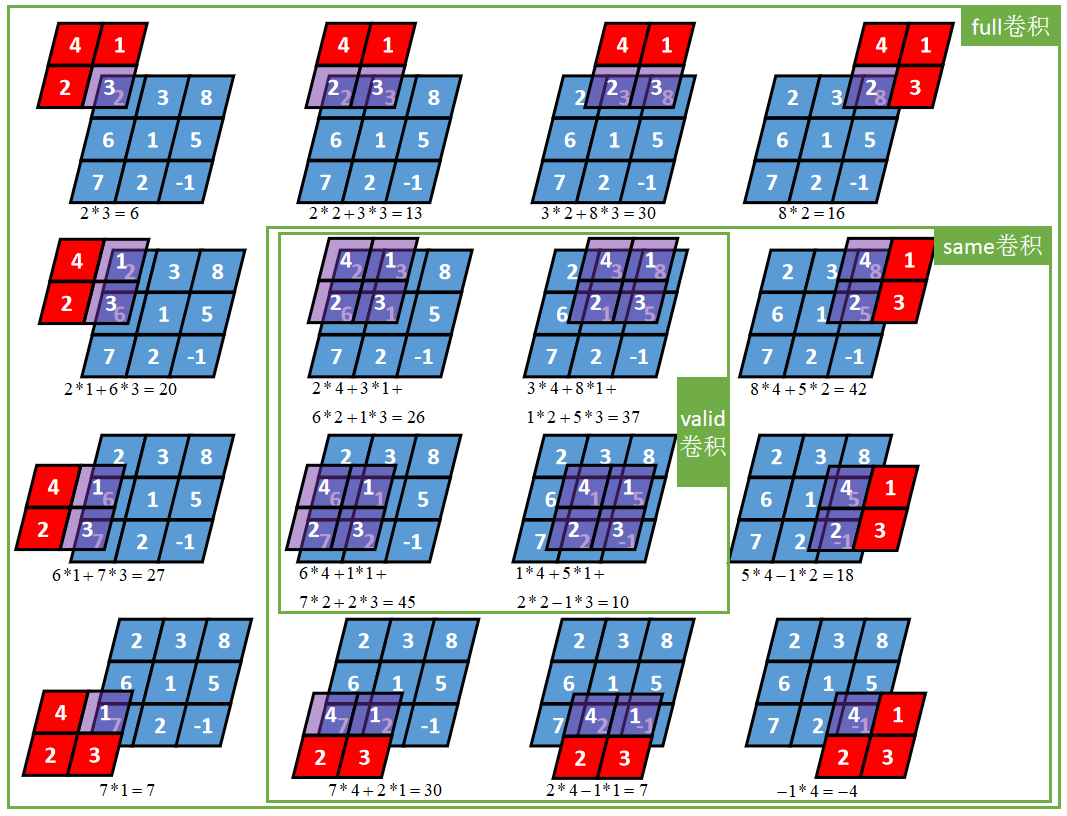
|
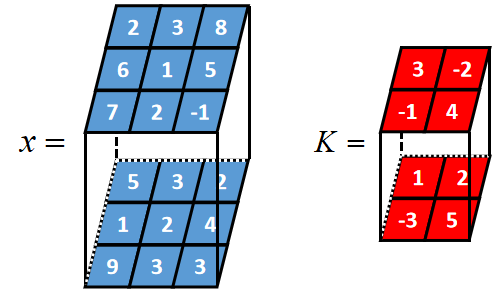
具备深度的二维卷积 |
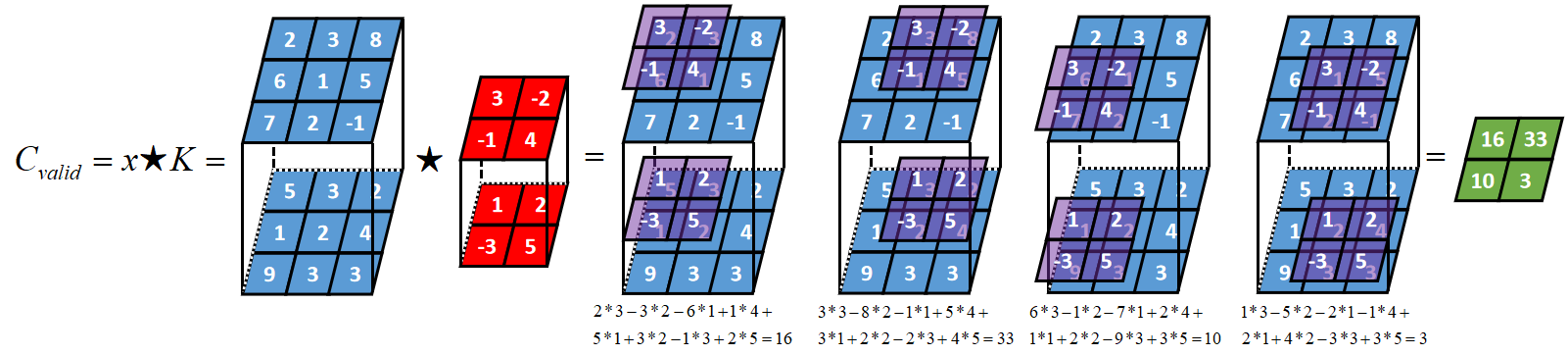
比如x是一个长度为3、宽度为3、深度为2的张量,卷积核K是一个长度为2、宽度为2、深度为2的张量,其valid卷积过程如下,卷积核K的锚点在张量x范围内从左到右,从上到下移动,输入张量的深度和卷积核的深度是相等的。
|
具备深度的张量与多个卷积核的卷积 |
1个3行3列2深度的x 与 3个2行2列2深度的卷积核卷积:

|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平