目录
导数
偏导数
方向导数
梯度
参考资料
|
导数 |
导数反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。
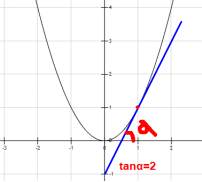
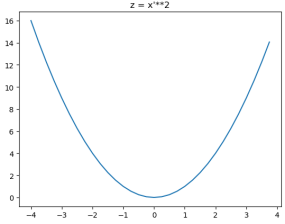
比如y=x2，在x=1处的导数=2。
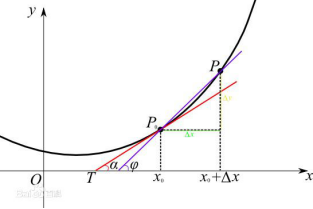
导数是通过极限来定义的，某一点的导数=tanψ，但是前提是△x趋近于0，此时tanψ=tanα=该点导数，公式如下：
|
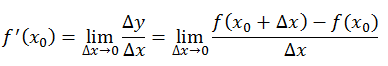
偏导数 |
在多元函数中，偏导数指的是函数y(x1,x2,…,xn)沿某一坐标轴(x1,x2,…,xn)正方向的变化率。
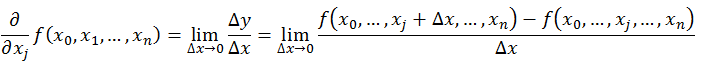
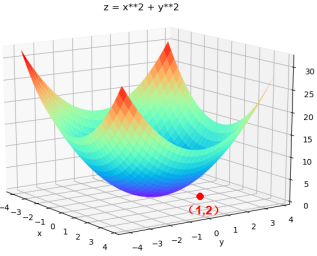
比如z=x2+y2，在(1,2)处的在x方向上的偏导数：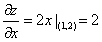
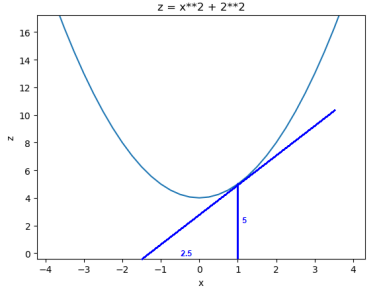
截取y=2的曲线，可以发现在x方向的导数=2
|
方向导数 |
导数和偏导数都是沿坐标轴正方向的变化率。那么当我们讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。
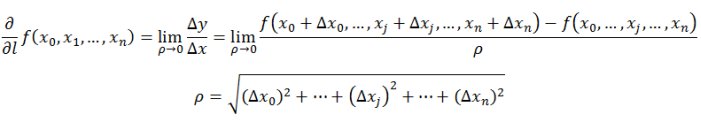
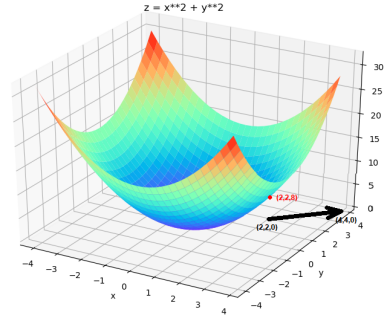
比如，可以计算函数在点A(2,2,8)处沿黑色箭头方向的导数。这里有两种计算方式：
方式1：
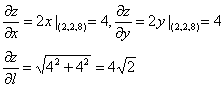
方式2：
与x=y联立方程组，得到过点A的剖面
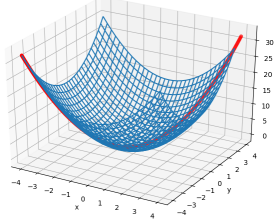
易知，剖面方程为z=2x2,以z为纵轴，x坐标轴方向换为L的方向，得到
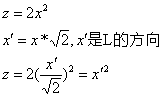
点A(2,2,8)在x’方向上的坐标为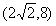
，因此在A点处沿L方向的导数为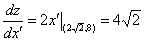
|
梯度 |
梯度是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
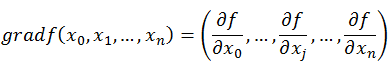
这里注意三点：
1）梯度是一个向量，即有方向有大小；
2）梯度的方向是最大方向导数的方向；
3）梯度的值是最大方向导数的值。
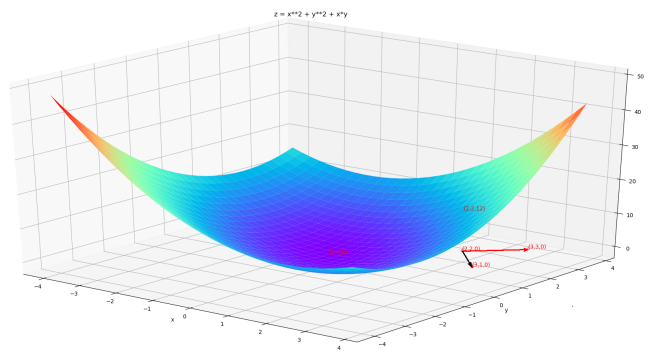
比如z=x2+y2+xy在点A(2,2,12)处的梯度为
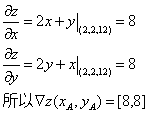
如图，在A点，红色方向是最大方向导数的方向，很明显红线方向的导数高于沿着黑线方向的导数。
那么A点的梯度方向是红色方向；A点的梯度值为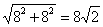
|
参考资料 |
[机器学习] ML重要概念：梯度（Gradient）与梯度下降法（Gradient Descent）
https://blog.csdn.net/walilk/article/details/50978864