汉诺塔

这是一个很典型的递归题目，有助于理解递归思想。

规则如下：

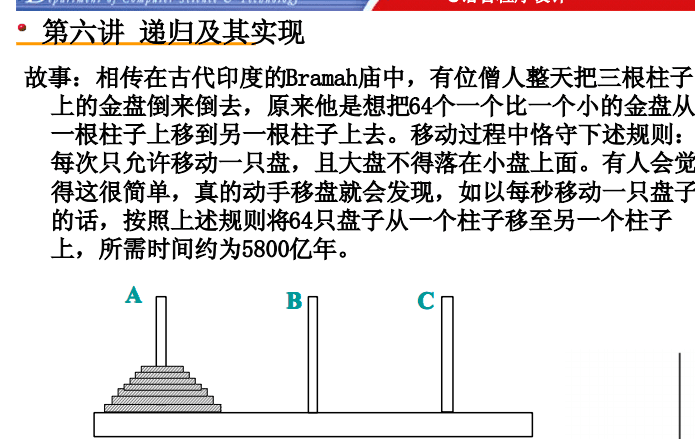
我们不妨自定义一个函数，用来移动盘

void hannuo(int n,char a,char b,char c) 含义：a上的n个盘子要通过b的中转移动到c上

好，那么这个函数怎么实现打印路径的功能呢？

  如果n==1那么直接把盘子从a移动到c上就行啦，所以打印a->c（需要注意的是这里的a、c都是参数，是变量）

  如果n!=1那么肯定有多于一个的盘子，那怎么把这n个盘子移动到c上呢？

      分为三步：第一步——把上面的n-1个盘子通过c的中转移动到b上（hannuo(n-1,a,c,b)）

　　　　　　  第二步——把最底下的盘子（现在已经是最上面的了）移动到c上（打印a->c）

　　　　　　  第三步——把b上的n-1个盘子再通过a的中转移动到c上（hannuo(n-1,b,a,c)）

如此，递归便完成啦。下面是代码：

#include<stdio.h>

void hannuo(int n,char a,char b,char c)
{
    if (1==n) {
        printf("%c->%c
",a,c);
    }
    else {
        hannuo(n-1,a,c,b);
        printf("%c->%c
",a,c);
        hannuo(n-1,b,a,c);
    }
}

int main()
{
    int k;
    scanf("%d",&k);
    hannuo(k,'a','b','c');
    return 0;
} 

再加深一下理解的话可以看这个图：

 

另外，如果只需要计算最小的移动步数的话直接用递推公式就行了。

f[1]=1

f[n]=f[n-1]*2+1

看懂了上面的递归函数的移动过程，这个公式也很容易理解啦。

再数学推导一下的话，可以直接用公式 f[n]=2^n-1