几种常见的排序小结

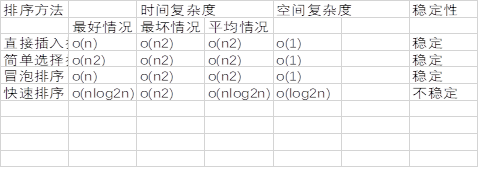
直接插入排序、简单选择排序、冒泡排序的优化、还有常用的快速排序，具体的注释也在代码中。

package cn.test.sort;

public class SortDemo {
	public static void main(String[] args) {
		int [] array= {0,32,12,34,5,7,19,80};
		straightInsertSort(array);
		print_array(array);
		simpleSelectSort(array);
		print_array(array);
		BubbleSort(array);
		print_array(array);
		quickSort(array, 0, array.length-1);
		print_array(array);
	}
	public static void print_array(int array[]) {
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i]+" ");
			if(i==array.length-1) {
				System.out.println(";");
			}
		}
	}
	//直接插入排序
	public static void straightInsertSort(int[] array)
	{
		int j,i,temp;  //temp 是临时变量 当后一项比前一项小的时候，就把后一项赋值给temp
		for(i=1;i<array.length;i++) {
			if(array[i]<array[i-1]) {
				temp = array[i];
				array[i] = array[i-1];	//当前的值要改变，让大的数在后面
				for(j=i-1;temp<array[j];j--) { //继续向前比较，如果还比前一个小就插入，
					array[j+1] = array[j];
				}
				array[j+1]  = temp;	//如果当前的数比前一个大就将临时变量赋值给当前位置
			}
		}
		
		
		return ;
	}
	//时间复杂度是O(n2),空间复杂度是O(1);
	
	//===============================================
	//简单选择排序	时间复杂度是O(n2),空间复杂度是O(1); 属于稳定排序

	public static void simpleSelectSort(int [] array)
	{
		if(array.length == 0) {
			return ;
		}
		for(int i=0;i<array.length;i++) {
			int k=i;
			for(int j=i+1;j<array.length;j++) {
				if(array[k]>=array[j]) {//第一躺，拿着第一个数与剩余的n-1个数比较，找出最小
									//的那个数，记录他的下标
					k=j;
				}	
			}
			if(k!=i) {	//如果这时的最小数的角标与之前的不一样，也就是说进入了循环，找到了比之前更小的
				int temp=array[k];//数，所以交换他们的位置，之后也是一样
				array[k] = array[i];
				array[i] = temp;
			}
		}
		
		return;
	}
	//================================================
	//冒泡排序的优化  稳定排序，时间复杂度是O(n2),空间复杂度是O(1);
	public static void BubbleSort(int[] array)
	{
		boolean flag ;
		for (int i = array.length-1; i >= 0; i--) {//比较n-1躺
			flag = false;//设置标志
			for (int j = 0; j < i; j++) {
				if(array[j]>array[j+1]) {//前面的数比后面大就交换位置
					int temp = array[j];
					array[j] = array[j+1];
					array[j+1] = temp;
					flag = true;//这趟有数交换就设置成true
				}
			}
			if(!flag) {//若没有交换就直接返回，不用在进行下一次的排序；例如原本一个有序数列不用在排
				return;
			}
		}
	}
	//快速排序 不稳定排序，时间复杂度O（nlog2n）空间复杂度最好O(log2n),最差是O(n)
	public static void quickSort(int [] array,int low,int hight) {
		if (array.length == 0 || low > hight||low<0||hight>array.length) {
			return ;
		}
		
		int i=low;
		int j = hight;
		int temp = array[low];	//将array[low]作为中轴，i，j当成“哨兵”
		//因为这里是将左边的第一个数当成枢轴，所以右边的j哨兵先走
			while(array[j]>temp&&i<j) {//j哨兵从后往前找，找到第一个小于temp(枢轴)的数的角标
				j--;
			}
			while(array[i]<temp&&i<j){
				i++;//i哨兵从前往后找，找到第一个比枢轴大的数，
			}
			if(i<j) {	//如果两个哨兵没有相遇就交换这两个数让大的数到右边，小的数在左边
				int t = array[i];
				array[i] = array[j];
				array[j] = t;
			
			}else {	//如果两个哨兵相遇了就代表这躺"巡逻"结束，这时交换枢轴的值array[low]和哨兵前面的值，将 
				array[low]=array[i];
				array[i] = temp;
				//其实temp = array[low];在上面
			}
		quickSort(array,low,hight-1);//同样的方法排左边的数
		quickSort(array,low+1,hight);//排右边的数
	}
	
	
	//快速排序的特点
		/*
		 * 快速排序记录非顺次的移动导致排序是不稳定的； 
		 * 排序过程要设置上届和下届，所以适用于顺序结构，很难用于链式结构
		 * 当n较大时，在平均情况下快排是所有内部方法中速度最快的一种，所以适合初始记录无序，n较大的情况。
		 */
}