问题引入
当我们需要对一组数据(无序)进行排序时,假设期末考试完了,老师要按照分数对大家的名次进行排序,这里假设五个同学分别考了 5分、3分、5分、2分、8分 (满分十分)。当然,我们一下子就看出了其中的奥妙,但是我们用程序该怎么写呢?
思路引导
我们可以创建一个大小为11的数组(因为这里统计的是0到10之间的数字出现次数),现在我们有11个变量,即从a[0]~a[10],刚开始我们将数组中所有的变量a[0]~a[10]的初始值设定为0(即这些分数没有人得过)。即a[0] = 0; 代表没人得过0分,a[1] = 0; 代表没人得过1分。
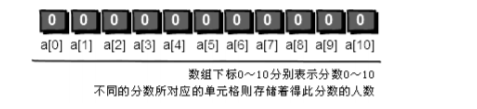
接下来我们开始处理每一个人的分数,若该分数出现一次,其对应的数组下标的值加一,即第一个同学的分数为5分,代表分数5出现一次,则相对应的a[5]++; 即现在a[5] = 1。

以此类推:第二个同学的分数为3分,此时3分出现一次,其对应的数组下标的值加一,则对应的a[3]++; 即a[3] = 1。

然后我们分别拿到2分,5分,8分(第三个同学的成绩也是5分,则a[5]原来值为1的基础上再加一,a[5]++; a[5] = 2)


一路分析下来,很明确,a[0]~a[10]中的数值就是0~10中每个分数出现的次数,接下载,我们只需要根据出现过分数的次数打印数组的下标(该分数)即可,出现几次就打印几次(比如5分出现两次,a[5] = 2,则将下标5打印两次)。

代码实现
#include "stdio.h"
int main()
{
//创建一个长度为11的数组,用来判断0-10数字出现的次数
int arr[11], i, j, n;
//将数组内所有下标值初始化为0,代表此数字出现0次
for (i = 0; i <= 10; i++) {
arr[i] = 0;
}
//循环读入五个0-10内的整数
for (i = 0; i < 5; i++) {
//将每个数读到变量n中
scanf("%d", &n);
//如果出现该数字,则对应的数组角标值加一
arr[n]++;
}
//第一层循环依次判断arr[0]-arr[10]中的值
for (i = 0; i <= 10; i++) {
//第二层循环判断该数字出现的次数,有几次就打印几次
for (j = 1; j <= arr[i]; j++) {
printf("%d", i);
}
}
}运行结果:
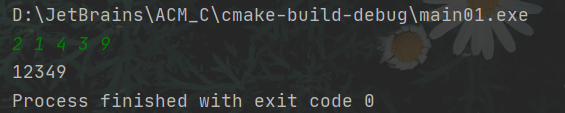
要想从大到小排序,将for (i = 0; i <= 10; i++)改为for (i = 10; i >= 0; i--)即可。
解析
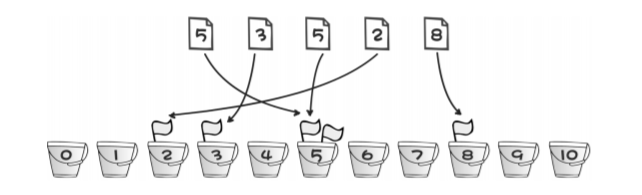
这个算法就好比有 11 个桶,编号从 0~10。每出现一个数,就在对应编号的桶中放一个 小旗子,最后只要数数每个桶中有几个小旗子就 OK 了。例如 2 号桶中有 1 个小旗子,表示 2 出现了一次;3 号桶中有 1 个小旗子,表示 3 出现了一次;5 号桶中有 2 个小旗子,表示 5 出现了两次;8 号桶中有 1 个小旗子,表示 8 出现了一次。
当然,我们可以想一下,这个算法是十分浪分空间的,当我们要统计要排序数的范围是 0~2100000000 之间,那你则需要申请 2100000001 个变量,也就是说要写 成 int a[2100000001]。因为我们需要用 2100000001 个“桶”来存储 0~2100000000 之间每一 个数出现的次数。即便只给你 5 个数进行排序(例如这 5 个数是 1、1912345678、2100000000、 18000000 和 912345678),你也仍然需要 2100000001 个“桶”,这真是太浪费空间了!还有, 如果现在需要排序的不再是整数而是一些小数,比如将 5.56789、2.12、1.1、3.123、4.1234 这五个数进行从小到大排序,这就显得无法实现了。
显然,简化版桶排序算法,其本质上还不能算是一个真正意义上的排序算法,其有很大的局限性,作为排序入门了解一下就可以了。
总结
简化版桶排序,用数组角标值从0自增的方式记录该角标(即输入的数字)出现的次数,然后遍历数组根据对应角标值的大小确认打印该角标的次数(即数字出现的次数)。
算法新手上车,请多指教!