地址 https://leetcode-cn.com/problems/maximal-square/
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:
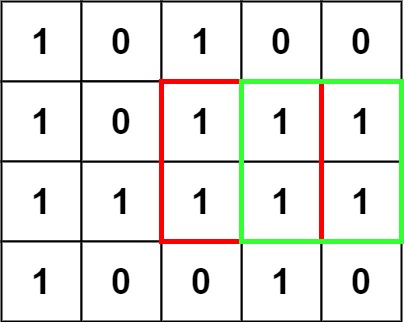
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:
输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'
解答
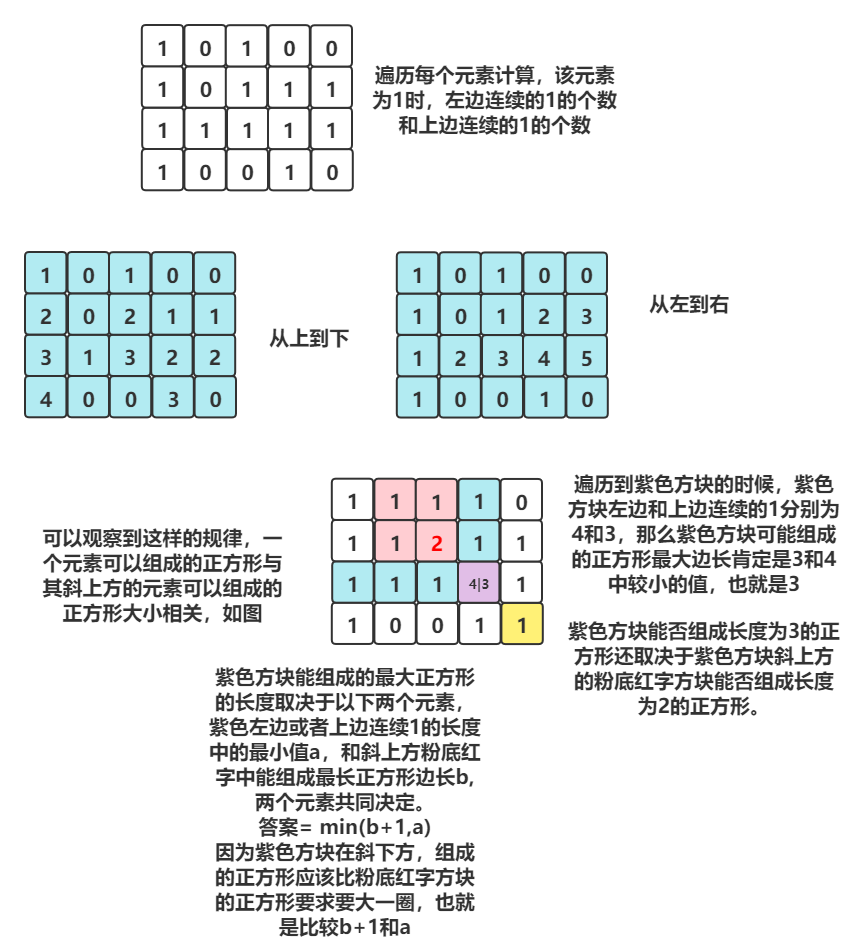
遍历矩阵记录每个元素1的左边的连续1 和每个元素1的上面的连续1
然后再次遍历矩阵 查看斜上角的1的能达到的最长长度
时间复杂度是O(n^2)
class Solution {
public:
int ans = 0;
int lr[310][310];
int ud[310][310];
void Check(const vector<vector<char>>& matrix,int dp[310][310], int x, int y)
{
int a1 = lr[x][y]; int a2 = ud[x][y];
int len = min(lr[x][y], ud[x][y]);
int prev = 0;
if (x - 1 >= 0 && y - 1 >= 0) {
prev = dp[x - 1][y - 1];
}
dp[x][y] = min(len,prev+1);
ans = max(ans, dp[x][y]);
}
int maximalSquare(vector<vector<char>>& matrix) {
int n = matrix.size(); int m = matrix[0].size();
if (m == 0 || n == 0) return 0;
memset(lr, 0, sizeof lr);
memset(ud, 0, sizeof ud);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == '0') { continue; }
if (i != 0) ud[i][j] = ud[i - 1][j] + 1;
else ud[i][j] = 1;
if (j != 0) lr[i][j] = lr[i][j - 1] + 1;
else lr[i][j] = 1;
}
}
int dp[310][310];
memset(dp,0,sizeof dp);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == '0') continue;
Check(matrix, dp,i, j);
}
}
return ans * ans;
}
};

