地址 https://leetcode-cn.com/problems/longest-valid-parentheses/
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
提示:
0 <= s.length <= 3 * 104
s[i] 为 '(' 或 ')'
解答
动态规划处理该题。
假设dp[i]表示从0~i的字符串以s[i]括号结尾能达到的最长括号子串的长度。
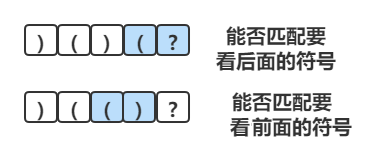
由于左括号需要查看后面的符号才能确认是否能括号配对
右括号是通过查看前面的符号就能确认能否配对,所以dp[i]有值的话 s[i]肯定是右括号 ')'
那么遍历字符串,如果当前是右括号则查看前一个符号是左括号还是右括号,不同情况不同处理
1 前一个符号是左括号
s[i]==')' s[i-1] == '('
那么dp[i]=2这时候继续查看s[i-2]是什么符号 看看这个匹配符号串能否继续增长
1.1 如果s[i-2]=='(' 那么这个匹配符号串无法继续增长,本轮检测结束
1.2 如果s[i-2]==')' 这时候dp[i-2] 已经计算出以s[i-2]结尾的能达到到的最长括号子串的长度。
我们加上该长度即可
dp[i] += dp[i-2]

2 前一个符号也是右括号
s[i]==')' s[i-1] == ')'
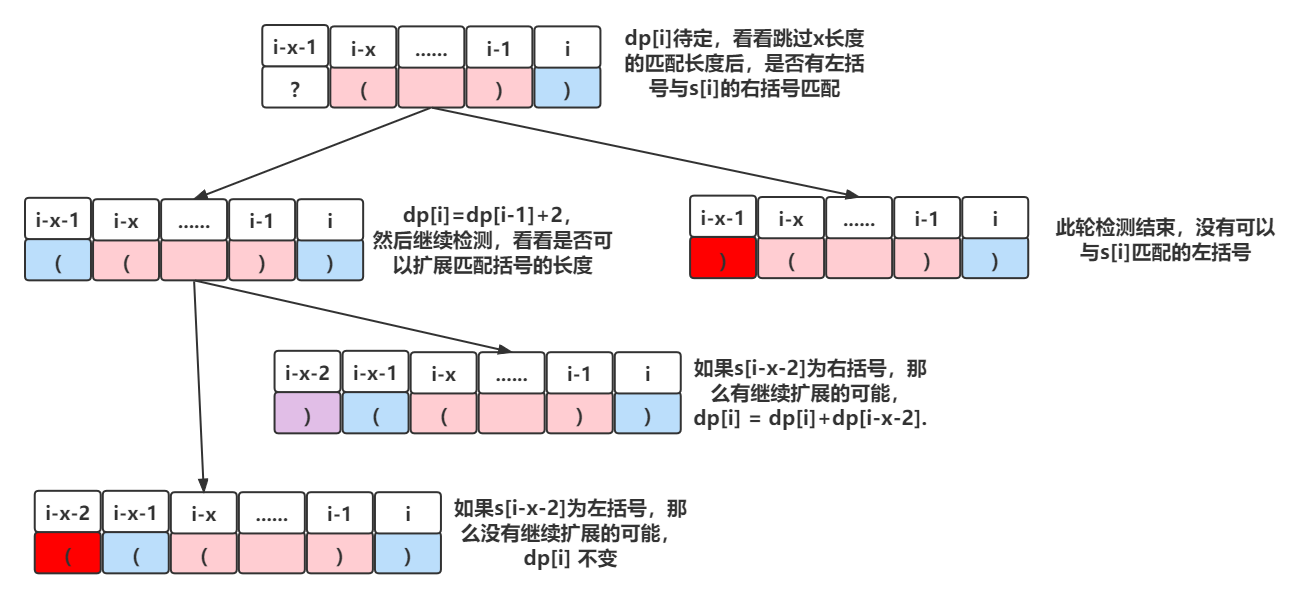
那么我们查看向左延续dp[i-1]长度的符号能否找到一个右括号和s[i]匹配(也就是略过dp[i-1]的配对字符串)
假设dp[i-1]=x
2.1 如果s[i-x-1]==')' 那么就无法匹配 本轮检测结束
2.2 如果s[i-x-1]=='(' 可以与s[i]匹配 dp[i]=dp[i-1]+2
这时候继续查看s[i-x-2]是什么符号 看看这个匹配符号串能否继续增长
效果同1.1 1.2
代码如下:
class Solution {
public:
int longestValidParentheses(string s) {
if (s.empty()) return 0;
int dp[30010] = { 0 };
for (int i = 0; i < s.size(); i++) {
if (i > 0 && s[i] == ')') {
//情况1
if (s[i - 1] == '(') {
dp[i] = 2;
if (i>=2 && s[i - 2] == ')') {
dp[i] += dp[i - 2];
}
}
else if (s[i - 1] == ')') {
//情况2
int t = dp[i - 1];
if ((i - 1 - t>=0) && s[i - 1 - t] == '(') {
dp[i] = t + 2;
if (i - 2 - t >= 0 && s[i - 2 - t] == ')') {
dp[i] += dp[i - 2 - t];
}
}
}
}
}
int ans = -99;
for (int i = 0; i < s.size(); i++) {
ans = max(ans, dp[i]);
}
return ans;
}
};
精简一点代码
class Solution {
public:
void CanIncrease(int dp[],const string&s,int curr,int idx){
if(idx>=0&& s[idx]==')'){ dp[curr] +=dp[idx];}
}
int longestValidParentheses(string s) {
if (s.empty()) return 0;
int dp[30010] = { 0 }; int ans = -1;
for (int i = 0; i < s.size(); i++) {
if (i > 0 && s[i] == ')'&& s[i - 1] == '(') {dp[i] = 2;CanIncrease(dp,s,i,i-2);}
else if (i > 0 && s[i] == ')'&& s[i - 1] == ')') {
//情况2
int t = dp[i - 1];
if ((i - 1 - t>=0) && s[i - 1 - t] == '(') {dp[i] = t + 2;CanIncrease(dp,s,i,i-2-t);}
}
ans = max(ans, dp[i]);
}
return ans;
}
};

