地址 https://www.papamelon.com/problem/327
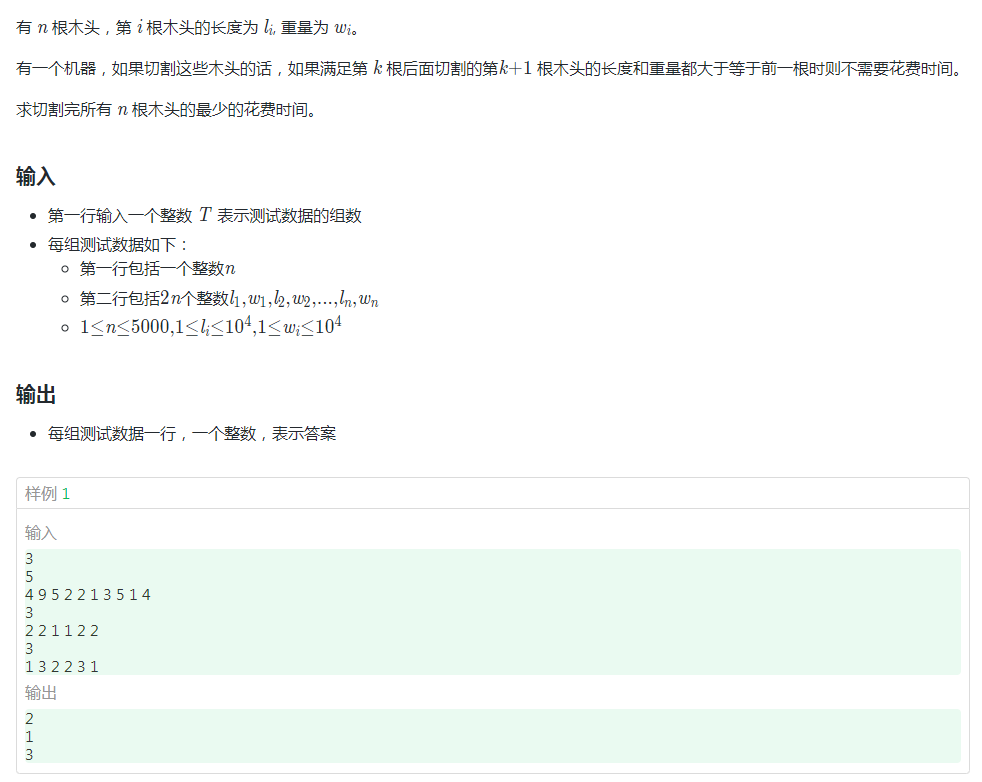
由于题目有两个排序关键字长度和重量,只有两个均大于等于前一个才能达到最小费用
先尝试按照某一个关键字排序
例子中的
4 5 2 3 1
9 2 1 5 4
排序后就变成
1 2 3 4 5
4 1 5 9 2
这时候我们就发现 排序后 第二行的关键字 按照最长不下降子序列切分后 就是最小费用了
比如说
1 3 4
4 5 9
但是如何得知最后能得到最少几组最长不下降序列?
这里就涉及到Dilworth定理
Dilworth定理:
通俗解释: 把一个数列划分成最少的最长不降子序列的数目就等于这个数列的最长下降子序列的长度(LIS)。
也就是solve2的解法 直接求最长下降子序列的长度。
//=========================================
solve3 贪心解法
按照以下思路进行解答
木棒有两个关键字属性 l=长度 w=重量。 木棒已经按照l进行排序
1 在已有的不降子序列中寻找序列尾部小于等于当前木棒w的序列,该序列是寻找出的序列中尾部最大的那个,在该序列尾部插入该木棒
2 如果没有找到合适的不降子序列 则新开一个序列。
3 持续 1 2过程 直到所有木棒都插入序列 序列个数则是答案
证明贪心解就是最优解
假设贪心解不是最优解答 另有最优解
那么在最优解和贪心解 在第一个木棒插入序列不同点之后的插入序列,都可以经过有限次调整进行互换。即,贪心解与最优解可以经过有限次调整进行互换,也就是相等。
那么贪心解就是最优解。
代码见solve3
代码
#include <iostream>
#include <algorithm>
#include <memory.h>
using namespace std;
const int N = 5010;
const int INF = 9999999;
struct STICK {
int l;
int w;
}stick[N];
int n, t;
bool cmpFunc(const struct STICK& a, const struct STICK& b) {
if (a.l < b.l) return true;
else if(a.l==b.l) return a.w < b.w;
return false;
}
void solve() {
int ans = 0;
for (int i = 0; i < n; i++) {
if (stick[i].w != INF) {
int curr = -INF;
for (int j = i; j < n; j++) {
if (curr == -INF && stick[j].w != INF) {
curr = stick[j].w; ans++;
}
else if (stick[j].w != INF && curr <= stick[j].w) {
curr = stick[j].w; stick[j].w = INF;
}
}
}
}
cout << ans << endl;
return;
}
void solve2() {
int dp[N]; memset(dp, 0, sizeof dp);
dp[0] = 1;
int ans = 0;
for (int i = 1; i < n; i++) {
dp[i] = 1;
for (int j = i - 1; j >= 0; j--) {
if (stick[i].w < stick[j].w) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
ans = max(ans, dp[i]);
}
cout << ans << endl;
return;
}
void solve3() {
int up[N]; int cnt = 0;
for (int i = 0; i < n; i++) {
int curr = -INF; int idx = -1;
for (int j = 0; j < cnt; j++) {
//找到up中小于等于 stick[i].w中最大的数 , 在其代表的序列中插入stick[i].w
//找不到则新建一个序列 插入stick[i].w
if (up[j] <= stick[i].w && curr < up[j]) {
idx = j; curr = up[j];
}
}
if (idx != -1) {
up[idx] = stick[i].w;
}
else {
up[cnt] = stick[i].w; cnt++;
}
}
cout << cnt << endl;
return;
}
int main()
{
cin >> t;
while (t--) {
cin >> n;
memset(stick,0,sizeof stick);
for (int i = 0; i < n; i++) {
cin >> stick[i].l >> stick[i].w;
}
sort(stick,stick+n,cmpFunc);
//solve();
//solve2();
solve3();
}
return 0;
}

