地址 https://leetcode-cn.com/problems/majority-element/
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3]
输出:3
示例 2:
输入:[2,2,1,1,1,2,2]
输出:2
进阶:
尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
解答
1 推断方法
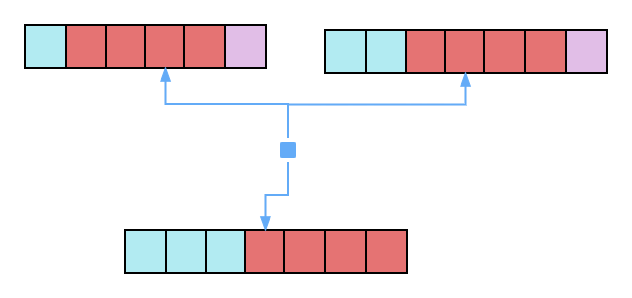
长度为n的数组中若有某个元素唱过一半[n/2]
那么这个数组的中间元素一定是该数 如图
class Solution {
public:
int majorityElement(vector<int>& nums) {
sort(nums.begin(),nums.end());
return nums[nums.size()/2];
}
};
2 哈希记录
class Solution {
public:
map<int,int> mm;
int majorityElement(vector<int>& nums) {
for(int i = 0; i<nums.size();i++){
mm[nums[i]]++;
}
for(auto& e:mm){
if(e.second>nums.size()/2) return e.first;
}
return 0;
}
};
3 摩尔投票
上述两种方法 在时间和空间复杂度上或多或少都有一些不满足题目要求
摩尔投票法可以时间复杂度为 O(n)、空间复杂度为 O(1) 要求解决该问题
比如有一组数字 用字母代替 x x y z m x x
我们从头遍历,计数为0的时候则记录当前数字且计数加1,遇到和记录相同的数字则计数加1 和记录不同的数字则count减1 .
摩尔投票的核心就是不同数字之间的消耗
无论y z m的计数是互相消耗 还是全部或者部分和x的计数消耗 最后剩下的记录的数字肯定是x
下面介绍下过程
1 开始计数为0 记录x 计数+1=1
2 x与记录相同均为x 计数+1=2
3 y与记录不同 计数-1= 1
4 z与记录不同 计数-1=0
5 计数=0 记录m 计数+1=1
6 x与记录不同 计数-1=0
7 计数=0 记录x 计数+1=1
答案为x
class Solution {
public:
int majorityElement(vector<int>& nums) {
int count = 0; int curr = -99999;
for (int i = 0; i < nums.size(); i++) {
if (count == 0) { curr = nums[i]; count++;}
else if (curr == nums[i]) {count++;}
else {count--;}
}
return curr;
}
};

