地址 https://www.acwing.com/problem/content/description/103/
有 N 头牛站成一行,被编队为 1、2、3…N,每头牛的身高都为整数。 当且仅当两头牛中间的牛身高都比它们矮时,两头牛方可看到对方。 现在,我们只知道其中最高的牛是第 P 头,它的身高是 H ,剩余牛的身高未知。 但是,我们还知道这群牛之中存在着 M 对关系,每对关系都指明了某两头牛 A 和 B 可以相互看见。 求每头牛的身高的最大可能值是多少。 输入格式 第一行输入整数 N,P,H,M,数据用空格隔开。 接下来 M 行,每行输出两个整数 A 和 B ,代表牛 A 和牛 B 可以相互看见,数据用空格隔开。 输出格式 一共输出 N 行数据,每行输出一个整数。 第 i 行输出的整数代表第 i 头牛可能的最大身高。 数据范围 1≤N≤10000, 1≤H≤1000000, 1≤A,B≤10000, 0≤M≤10000 输入样例: 9 3 5 5 1 3 5 3 4 3 3 7 9 8 输出样例: 5 4 5 3 4 4 5 5 5 注意: 此题中给出的关系对可能存在重复
解答
两头牛可以看到对方 他们之间的牛就需要减少预期高度
连续区间减少某数值,考虑使用差分
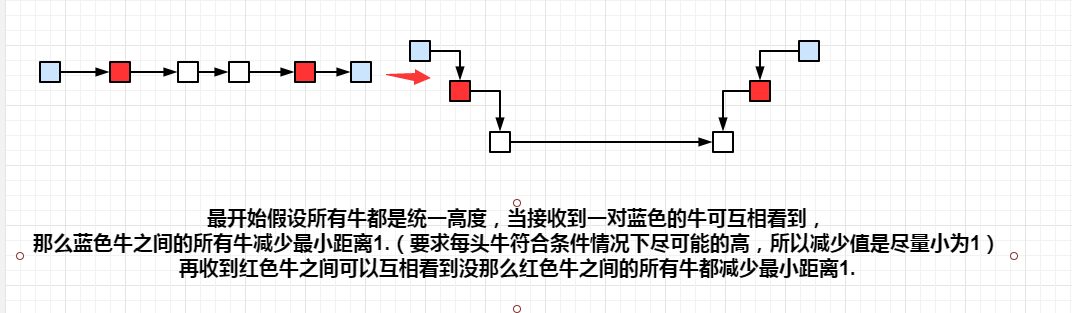
解决差分问题后 还有个输入细节问题
由于输入可能有重复输入 我们不能每次收到一对牛可以互相看到就将其之间的牛的预期高度减少
这样会造成重复减少,所以使用了set<pair<int,int>>进行去重
最后就是 使用到差分数组的前缀和就是原数组这个知识点
我们将已经处理完毕的差分数组 进行前缀和相加 得到原数组也就是每头牛的高度,进行输出即可
#include <iostream> #include <algorithm> #include <set> using namespace std; const int N = 10010; int arr[N]; int n,p,h,m; set<pair<int, int>> mm; int main() { cin >> n >> p >> h >> m; arr[1] = h; for (int i = 0; i < m; i++) { int a; int b; cin >> a >> b; if (a > b) swap(a, b); if (mm.count({ a,b }) == 0) { mm.insert({ a,b }); arr[a + 1]--; arr[b]++; } } for (int i = 1; i <= n; i++) { arr[i] += arr[i - 1]; cout << arr[i] << endl; } return 0; }

