地址 https://leetcode-cn.com/problems/maximum-absolute-sum-of-any-subarray/
给你一个整数数组 nums 。一个子数组 [numsl, numsl+1, ..., numsr-1, numsr] 的 和的绝对值 为 abs(numsl + numsl+1 + ... + numsr-1 + numsr) 。 请你找出 nums 中 和的绝对值 最大的任意子数组(可能为空),并返回该 最大值 。 abs(x) 定义如下: 如果 x 是负整数,那么 abs(x) = -x 。 如果 x 是非负整数,那么 abs(x) = x 。 示例 1: 输入:nums = [1,-3,2,3,-4] 输出:5 解释:子数组 [2,3] 和的绝对值最大,为 abs(2+3) = abs(5) = 5 。 示例 2: 输入:nums = [2,-5,1,-4,3,-2] 输出:8 解释:子数组 [-5,1,-4] 和的绝对值最大,为 abs(-5+1-4) = abs(-8) = 8 。 提示: 1 <= nums.length <= 105 -104 <= nums[i] <= 104
算法1
(动态规划) O(n)
子数组的最大和的abs版本
遍历两次
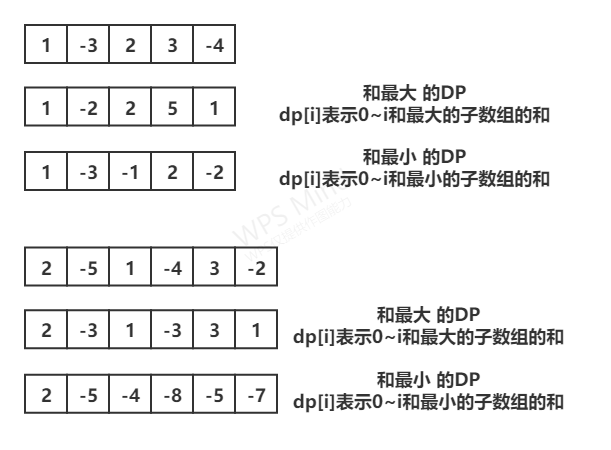
1 使用动态规划记录数组0~i的和的最大值 dpPos[i] = max(dpPos[i-1]+nums[i],nums[i]);
2 使用动态规划记录数组0~i的和的最小值(可能 abs后 最大) dpNeg[i] = min(dpNeg[i-1]+nums[i],nums[i]);
class Solution { public: int dpNeg[100010]; int dpPos[100010]; int maxAbsoluteSum(vector<int>& nums) { nums.insert(nums.begin(),0); int ansMax= -9999999; int ansMin= 9999999; for(int i = 1; i < nums.size();i++){ dpPos[i] = max(dpPos[i-1]+nums[i],nums[i]); ansMax = max(ansMax,dpPos[i]); } for(int i = 1; i < nums.size();i++){ dpNeg[i] = min(dpNeg[i-1]+nums[i],nums[i]); ansMin = min(ansMin,dpNeg[i]); } return max(ansMax,abs(ansMin)); } };

