地址 https://leetcode-cn.com/problems/magnetic-force-between-two-balls/
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。 Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。 已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。 给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
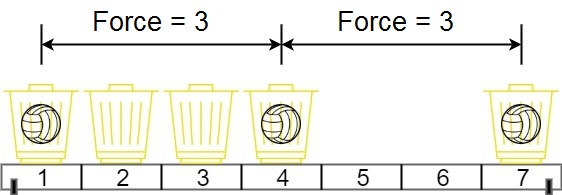
示例 1: 输入:position = [1,2,3,4,7], m = 3 输出:3 解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。 示例 2: 输入:position = [5,4,3,2,1,1000000000], m = 2 输出:999999999 解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
算法1
(二分) O(nlogn)O(nlogn)
最小磁力最小 等于两球最短距离最大
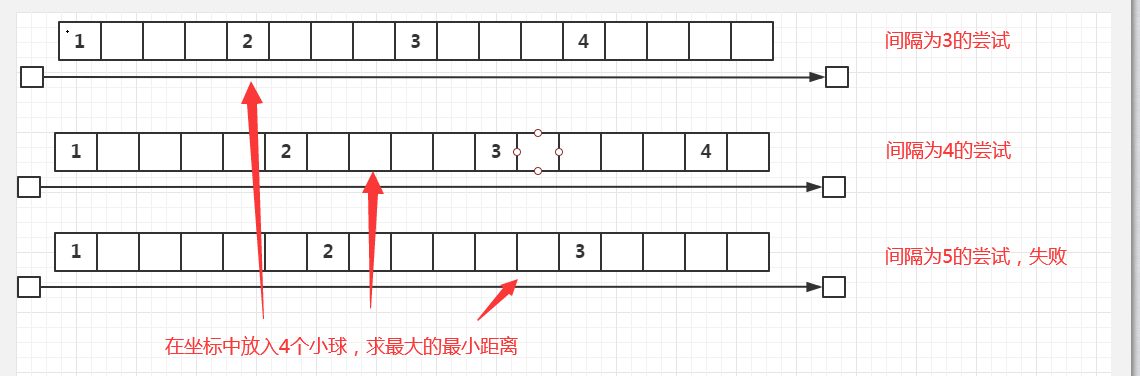
比如说我们假设最小距离是3 那么两球间的距离至少是3不会低于3,否则3就不可能是最小距离。
如果在最小距离是3的情况可以放置,那么我们就尝试最小距离为4的放置方案,
然后尝试最小间隔为5
在可放置完成与不可放置完成之间的距离就是答案。
这是一个区间划分的问题 可以使用二分解决
class Solution { public: bool check(vector<int>& position,int distance,int m){ int pos = position[0]; m--; for(int i = 1;i < position.size();i++){ if(m==0) return false; if(position[i]-pos >= distance ){ pos = position[i];m--; } } if(m ==0) return false; else return true; } int maxDistance(vector<int>& position, int m) { sort(position.begin(),position.end()); int l =0; int r = position[position.size()-1]; while(l< r){ int mid = l+r >>1; if(check(position,mid,m)) r= mid; else l= mid+1; } return r-1; } };

