地址 https://leetcode-cn.com/problems/range-sum-query-mutable/
题目描述
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
update(i, val) 函数可以通过将下标为 i 的数值更新为 val,从而对数列进行修改。
示例: Given nums = [1, 3, 5] sumRange(0, 2) -> 9 update(1, 2) sumRange(0, 2) -> 8 说明: 数组仅可以在 update 函数下进行修改。 你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。
算法1
区间求和 自然使用 线段树 或者线段数组
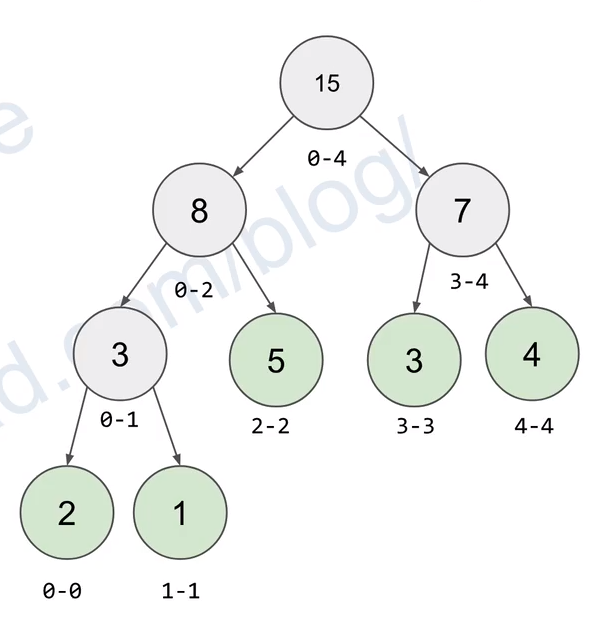
这里以线段树为例
以 空间换时间 记录线段之间的和 最大最小值等
由于是树 即使其中一部分元素改变或者某一个元素改变 更改记录也只是log(n)的复杂度
class SegmentTreeNode { public: SegmentTreeNode(int start,int end,int sum, SegmentTreeNode* left = nullptr, SegmentTreeNode* right = nullptr): start(start), end(end), sum(sum), left(left), right(right){} SegmentTreeNode(const SegmentTreeNode&) = delete; SegmentTreeNode& operator=(const SegmentTreeNode&) = delete; ~SegmentTreeNode() { delete left; delete right; left = right = nullptr; } int start; int end; int sum; SegmentTreeNode* left; SegmentTreeNode* right; }; class NumArray { public: NumArray(vector<int> nums) { nums_.swap(nums); if (!nums_.empty()) root_.reset(buildTree(0, nums_.size() - 1)); } void update(int i, int val) { updateTree(root_.get(), i, val); } int sumRange(int i, int j) { return sumRange(root_.get(), i, j); } private: vector<int> nums_; std::unique_ptr<SegmentTreeNode> root_; SegmentTreeNode* buildTree(int start, int end) { if (start == end) { return new SegmentTreeNode(start, end, nums_[start]); } int mid = start + (end - start) / 2; auto left = buildTree(start, mid); auto right = buildTree(mid + 1, end); auto node = new SegmentTreeNode(start, end, left->sum + right->sum, left, right); return node; } void updateTree(SegmentTreeNode* root, int i, int val) { if (root->start == i && root->end == i) { root->sum = val; return; } int mid = root->start + (root->end - root->start) / 2; if (i <= mid) { updateTree(root->left, i, val); } else { updateTree(root->right, i, val); } root->sum = root->left->sum + root->right->sum; } int sumRange(SegmentTreeNode* root, int i, int j) { if (i == root->start && j == root->end) { return root->sum; } int mid = root->start + (root->end - root->start) / 2; if (j <= mid) { return sumRange(root->left, i, j); } else if (i > mid) { return sumRange(root->right, i, j); } else { return sumRange(root->left, i, mid) + sumRange(root->right, mid + 1, j); } } };

