http://acm.hdu.edu.cn/showproblem.php?pid=6121
【题意】
- 询问n个结点的完全k叉树,所有子树结点个数的异或和是多少
【思路】
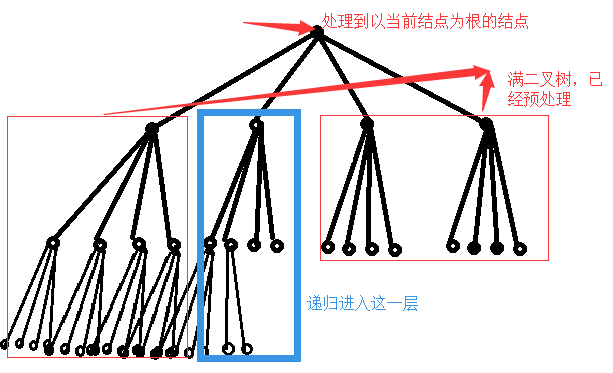
- 一棵完全K叉树,对于树的每一层,我们可以分为三种结点:
- 满k叉树的结点
- 不满的k叉树
- 比第一种情况少一层的满结点的k叉树
【AC】

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll n,k; 5 ll ans; 6 ll kn[70],sz[70],full[70]; 7 int cs; 8 void Pre() 9 { 10 //kn[i]=k^i 11 kn[0]=1; 12 for(int i=1;i<=cs;i++) 13 { 14 kn[i]=kn[i-1]*k; 15 } 16 //根结点为第一层,sz[i]为有i层的满k叉树有多少结点 17 sz[1]=1; 18 for(int i=2;i<=cs;i++) 19 { 20 sz[i]=sz[i-1]+kn[i-1]; 21 } 22 //有i层的满k叉树所有子树结点大小的异或和 23 if(k&1) 24 { 25 full[0]=0; 26 for(int i=1;i<=cs;i++) 27 { 28 full[i]=full[i-1]^sz[i]; 29 } 30 } 31 else 32 { 33 for(int i=1;i<=cs;i++) 34 { 35 full[i]=sz[i]; 36 } 37 } 38 } 39 40 void dfs(int cur) 41 { 42 ans^=n; 43 ll lft=n-sz[cur]; //最后一层有多少个 44 ll l=lft/kn[cur-1];//多少个cur层的满k叉树 45 lft-=l*kn[cur-1]; 46 if(lft==0)//没有不满的k叉树 47 { 48 if(l&1) ans^=full[cur]; 49 if((k-l)&1) ans^=full[cur-1]; 50 return; 51 } 52 if(l&1) ans^=full[cur]; 53 if((k-l-1)&1) ans^=full[cur-1]; 54 n--;n-=l*sz[cur];n-=(k-l-1)*sz[cur-1]; 55 dfs(cur-1); 56 } 57 int main() 58 { 59 int T; 60 scanf("%d",&T); 61 while(T--) 62 { 63 ans=0; 64 scanf("%I64d%I64d",&n,&k); 65 //k=1特判,打表看出来的 66 if(k==1) 67 { 68 if(n%4==0) 69 { 70 ans=n; 71 } 72 else if(n%4==1) 73 { 74 ans=1; 75 } 76 else if(n%4==2) 77 { 78 ans=n+1; 79 } 80 else 81 { 82 ans=0; 83 } 84 printf("%I64d ",ans); 85 continue; 86 } 87 //根结点为第一层,结点数为n的完全k叉树有cs层是满的 88 cs=0; 89 ll t=n; 90 while(t) 91 { 92 t--; 93 t/=k; 94 cs++; 95 } 96 //预处理 97 Pre(); 98 ans=0; 99 //递归 100 dfs(cs); 101 printf("%I64d ",ans); 102 } 103 return 0; 104 }
