描述:https://www.luogu.com.cn/problem/P1790
有一个长为a,宽为b的矩形(1≤a≤6,2≤b≤6)。可以把这个矩形看作是a*b个小方格。
我们现在接到了这样的一个任务:请你计算出,把这个矩形分割成两个部分的方法总数。
你不是可以任意地分割这个大的矩形, 必须满足:
分割后,每个部分,至少各自均有一个方格是在大矩形的最外边上(即大矩形最外面一环的方格)。
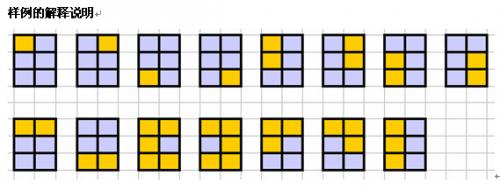
摘自 ywwuyi
- 这道题的思路实际非常简单
- 一个由ab个小矩形组成的矩形
- 事实上可以看成一个由(a+1)(b+1)个点组成的点图
- 那么题目就可以转换为从一个边缘上的点出发,到另一个边缘点,一共有几个方案
- 为了避免重复方案的出现,我们将出发点设置在最左及最上的边上(或者最右和最下的边)
- 接下来考虑无效切割的处理(如切割(1,1)与(2,1)之间的边,这样图依然只有一个),显然,如果我们直接从边缘点开始搜索,无效切割的出现是必然的,所以我们需要做一些处理
- 首先,不将矩形的四个顶点(即边与边的交点)作为出发点,因为从顶点出发必然会导致无效切割
- 其次,我们手动将出发点走到点阵内(如从(1,1)到(1,2)),然后再进行搜索,就可以避免无效切割。这时可能会有人问,如果"手动走到的那个点"也是边缘点怎么办?我们只需要把关于边缘点的判断写在dfs开头即可。
- 最后,跳出搜索的条件就是当前位置再次到达边缘点,答案+1,回溯
- 值得注意的是,n是长m是宽,在这题当中长是竖着摆的,所以x应该是与n配对
-
#include <bits/stdc++.h> using namespace std; int n,m,vis[10][10],ans; int b[5]={0,0,1,-1},c[5]={1,-1,0,0}; void dfs(int x,int y) { if(x==1||y==1||x==n||y==m){ ans++; return; } for(int i=0;i<4;i++) { int nx=x+b[i],ny=y+c[i]; if(nx<1||ny<1||nx>n||ny>m) continue; if(vis[nx][ny]) continue; vis[nx][ny]=1; dfs(nx,ny); vis[nx][ny]=0; } } int main() { cin>>m>>n;//转换为点图时n+1,m+1 n++;m++;//长和宽 for(int i=2;i<n;i++)//那么处理1和n+1,都枚举一次 { memset(vis,0,sizeof(vis)); vis[i][1]=vis[i][2]=1; dfs(i,2); } for(int i=2;i<m;i++) { memset(vis,0,sizeof(vis)); vis[1][i]=vis[2][i]=1; dfs(2,i); } cout<<ans; }