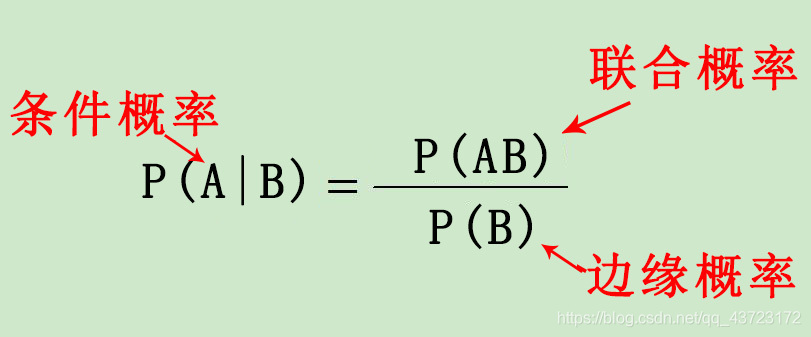深入学习机器学习、分布式算法才发现概率与统计,线代都很重要,下面我简单串一下如题目所示的知识
第一步:
P(A|B)是在条件B发生的情况下A发生的概率,P(AB)是条件A与B同时发生的概率。
关于条件概率、联合概率的例子我在最后一步骤举出,如独立事件和古典概型都懂,则请跳至最后一步看例子
先记牢靠公式:
在这里,可以按照下图来理解:
P(AB)等于图中的A交B的部分的概率,而P(A|B)等于A交B的面积的占B空间的比值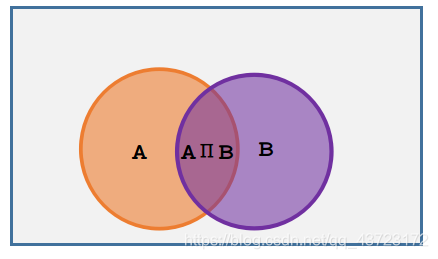
第二步:
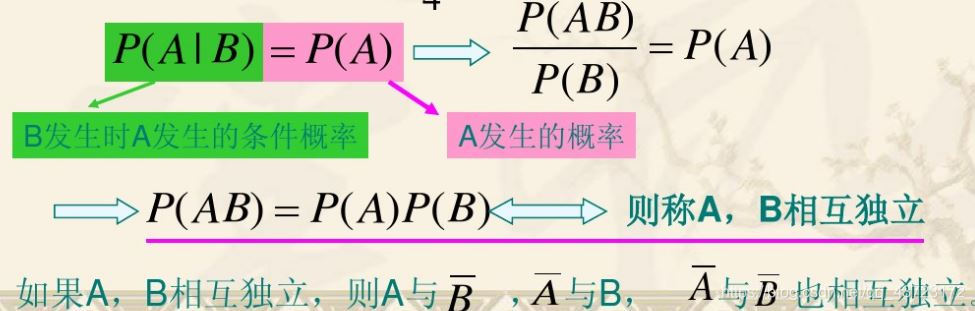
独立事件即是指两个事件的发生不互相影响
例子: 今天我上街的概率是1/3,不上街的概率是2/3;你上街的概率是2/3,不上街的概率是1/3。则可设A事件为我上街,B事件为你上街,则P(A)=1/3 , P(B)=2/3,也有P(A|B)=P(AB)/P(B)=(1/3 * 2/3)/(2/3)=1/3=P(A)
而独立事件本身有的性质就为:
第三步:
古典概型的特点:有限性和等可能性
例子: 盒子中有完全一样的10个球,其中6白,4黑,不放回的抽取两次,每次任取一球,求下列事件的概率:
(1)第二次才抽得白球(2)第二次抽得白球(3)至少有一个白球(4)如果已经发现有一个白球,求另一个也是白球的概率
解答:
(1)第二次才抽得白球:
也就是说,第一次抽得的不是白球,即第一次抽得黑球并且第二次抽得白球
第一次抽得黑球的概率是:4/10,
在第一次抽得黑球的前提下,第二次抽得白球的概率:6/9
所以第二次才抽得白球的概率:4/106/9 = 4/15
(2)第二次抽得白球:
包括第一次抽得白球和第一次抽得黑球两种情况,所以
第二次抽得白球的概率:4/106/9 + 6/105/9 = 3/5
(3)至少有一个白球:
就不用分第一次和第二次了。但包括了恰有2个白球和恰有1个白球
恰有1个白球的概率是 6/104/9+4/106/9= 8/15
恰有2个白球的概率是6/105/9= 1/3
所以至少有一个白球的概率是8/15+1/3 = 13/15
或者可以从反方面来,至少有一个白球的的反面是一个白球都没有,全是黑球。抽两次都是黑球的概率为:4/10*3/9=2/15
所以至少一次白球的概率为1-2/15=13/15
(4)相当于5个白球4个黑球中任取1个白球的概率:5/9
第四步(最后一步):
例子: 盒子中有完全一样的6个球,其中2红,3黑,1白。不放回抽取两次,求第一次摸出黑球的前提下,第二次摸出红球的概率
解答: 可设事件A为:第一次摸出黑球;事件B为:第二次摸出红球。那么问题变为求取P(B|A)
那么
P(A)的概率为:3/6 = 1/2
P(AB)表示为第一次摸出黑球 且 第二次摸出红球的概率,概率为:(3/6) * (2/5)=1/5
P(B|A)表示在第一次摸出黑球 的前提下 ,第二次摸出红球的概率,概率为(1/5)/(1/2)=2/5 (这是公式得出的结果,我们自己来验证一下:既然第一次已经确定摸出黑球了,那第二次摸之前盒子里面只有五个球了,此时红球有两个,黑球两个,白球一个,所以第二次摸出红球的概率为2/5。结果是对的)
总结:
条件概率是针对 缩减了的样本空间 的(本例中,因为是在事件A发生的前提下发生的,所以条件概率针对的样本空间直接就是5;所以P(B|A)发生的概率为2/5)
联合概率是针对 整个样本空间 的(此例的样本空间为6,因为有6个球),联合概率是指满足事件A又同时满足事件B的概率(本例中最开始样本空间为6,所以事件A的概率为3/6;满足了A事件之后,此时样本空间才减少至五个,所以P(AB)发生的概率就是2/5;所以P(AB)才是3/6 * 2/5 =1/5)
边缘概率是相对联合概率的而言,只极端的考虑其中一个变量,比如本例中P(A)= 3/6 。拓展一下: 如果需要我们求取P(B)的话,应该怎么办。首先搞清楚P(B)指的是第二次摸到红球的概率,那第一次可以摸到白球也可以摸到红球也可以摸到黑球,所以分三种情况:(1)第一次摸到红球:2/6 * 1/5 =1/15 (2)第一次摸到黑球:3/6 * 2/5 = 1/5 (3)第一次摸到白球:1/6 * 2/5 =1/15。 所以P(B)= 1/15 + 1/5 +1/15 =1/3
最后拓展一下: 已经求取边缘概率P(B),那么问题如果改为求第二次摸到红球的前提下,第一次摸到黑球的概率(即求P(A|B))的话。解为:P(A|B) = P(AB)/P(B)=3/5( 这是公式得出的结果,我们自己又来验证一下:既然第二次必须要取出红球,那第一次就只能从一个红球,三个黑球,一个白球中取了,此时总共可以选的球的数量为5,而要求第一次取黑球,所以第一次取出黑球的概率为3/5,结果是对的)
原文:https://blog.csdn.net/qq_43723172/article/details/104828221