atcoder上的题虽然有的很水,但是还是很有点东西的
即使是难度还不如CFDiv3的Abc,后两道题也是非常有启发性
这道题就是一个典型的例子
题意:
在一个h*w的棋盘上,车在(1,1)的位置,棋盘上有m个阻碍,请问车走两步以内能够覆盖的路径有多少个格子
数据范围:棋盘大小2e5*2e5,障碍物数量2e5
题解:
首先想到,车要在两步以内走到尽量多的格子,必然向右走一步,向下走一步,或者先向下,再向右。
显然,任何障碍物都会堵上自己右方和下方所有格子的其中一条路。
那么,车走不到的格子,就必然是先右再下,先下再右的路径都被堵上。
在下图中,浅红色格子就是其中一条路径被堵上了,深红色就是两条都被堵上了
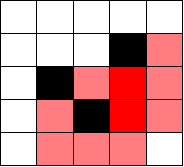
再考虑是稀疏矩阵,依次遍历,用树状数组维护右下路径被堵住的列,将被右下路径堵住的格子数排除出答案,然后对于每一行,在树状数组上求区间和,算出下右路径能补偿回多少个被堵住的格子。
慢着,考虑这种情况没有:
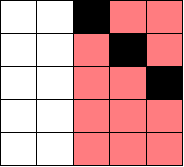
在这种情况下,右上角的三个格子显然无法到达,但是用上面那种方法分析,似乎只被堵住了下右路径,右下路径还是畅通的,但是实际上,右下路径在向右移动时就被第一列的格子堵住了,所以,当有障碍物处于第一行或者第一列的时候,要考虑特殊情况。赛后我想出的方法是,添加虚拟的障碍物。
像这样,灰色标志虚拟障碍物
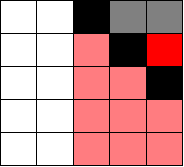
或者这样
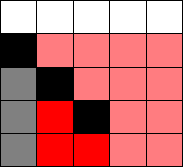
但是在添加虚拟障碍物之后,要记得数组范围,并且要去重。
代码:
#include<iostream> #include<algorithm> #define lowbit(a) ((a)&-(a)) #define LL long long using namespace std; struct Point{ int x,y; friend bool operator < (const Point &a,const Point &b){ return a.x==b.x?a.y<b.y:a.x<b.x; } friend bool operator ==(const Point &a,const Point &b){ return a.x==b.x && a.y==b.y; } }p[600005]; int c[200005]; int a[200005]; void update(int x,int y,int n){ for(int i=x;i<=n;i+=lowbit(i)) c[i] += y; } int getsum(int x){ int ans = 0; for(int i=x;i;i-=lowbit(i)) ans += c[i]; return ans; } int main(){ int h,w,m; scanf("%d %d %d",&h,&w,&m); int upx=h+1,upy=w+1; for(int i=1;i<=m;i++){ scanf("%d %d",&p[i].x,&p[i].y); if(p[i].x==1)upy=min(upy,p[i].y); if(p[i].y==1)upx=min(upx,p[i].x); } for(int i=upx+1;i<=h;i++){ m++; p[m].x=i;p[m].y=1; } for(int i=upy+1;i<=w;i++){ m++; p[m].y=i;p[m].x=1; } sort(p+1,p+1+m); m=unique(p+1,p+1+m)-p-1; int lst=1; LL ans=0; for(int i=1;i<=m;i++){ //纵向构造 if(a[p[i].y]==0){ a[p[i].y]=1; update(p[i].y,1,w); } if(i==m || p[i+1].x!=p[i].x){ //横向搜索 ans+=getsum(w)-getsum(p[lst].y-1); lst=i+1; } } printf("%lld ",1LL*h*w-ans); return 0; }