1、综述
PGM的学习问题实际上是对参数进行推断。对于给定的数据,需要求出系统参数,从而完善系统的CPD。但是某些情况下,PGM的数据集可能是不完整的。数据集不完整可以分为两种情况:1、数据采集受到了影响;2、使用了隐变量。数据采集受到影响可能出于两种情况,第一种是影响与被采集数据是无关的,例如投硬币,结果硬币找不到了。第二种是和被采集数据有关的,例如在收发数据时,高电平总是踩空。故在使用不完整的数据对模型进行训练之前,需要对造成不完整的原因进行判断。如果对上述两种情况进行建模,则有以下图模型:

其中,theta是系统参数,y是数据集,O是观测变量(O=1,观测;)。
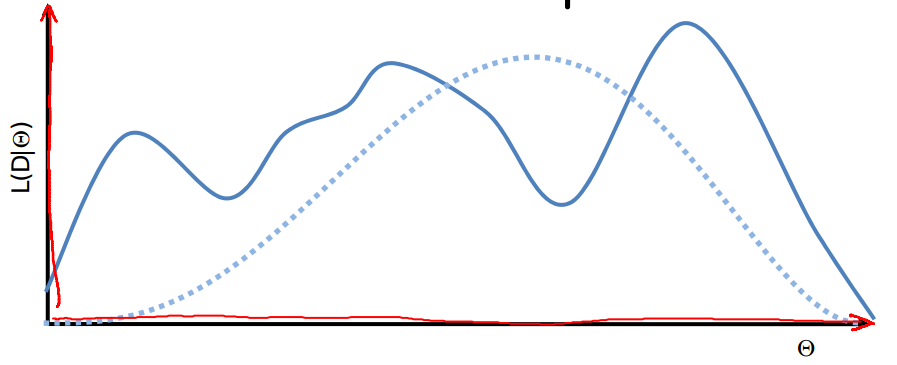
如果系统参数在没有先验的情况下,应该使用likelihood函数对系统参数进行推测。以简单的CPD为例,不完整数据与完整数据的likelihood对比如下图所示:


显然在数据完整的情况下,参数之间是不存在耦合的,我们可以分别对theta_x与theta_y,进行优化求解。很好理解,数据一旦被观测到,那么参数之间的trait就被堵死了。但是如果数据是不完整的,那么theta_x与theta_y则耦合了,不能分别优化。因为var_x没有被完全观测到,theta_y与theta_x之间存在通路。分析似然函数可知,其存在多个峰。系统参数的辨识更加困难了。
2、基于似然函数优化的参数辨识
似然函数存在多个峰,且有局部最优值。但是如果要获得一组有意义的参数还能有什么办法?只能求似然函数的最值。归根结底的思想还是该组参数使得数据发生的可能性最大。所以,可以使用优化方法来对似然函数进行求解。最简单的——梯度下降法。
其梯度解析解如下所示:

其核心是计算P(xi,ui|d[m],theta).此概率可通过标定团树获得。
优化算法的优点是:很灵活,可以用于所有的CPD,包括非表类CPD.缺点是:该算法是条件优化的,需要保证所有参数之间不矛盾。并且每次更新参数都要重新标定团树。
3、最大期望算法
最大期望算法的思想其实很简单,我们拿到数据的目标是为了推测系统参数;但是数据不完全,如果我们有了系统参数,就可以把数据推测完全。所以这是个循环的过程,事实证明,不断的循环迭代可以使得最终参数估计逼近真实系统参数。

在E-step中,假设已知系统参数theta,在给定theta的情况下,对所有的可能的组合x,u求取其概率。完整数据则求完整概率,不完整数据则求其边际缺失变量后概率。在M-step中,再利用充分统计对系统参数theta进行更新。
比如在贝耶斯分类器中,我们只有数据而没有数据的class值。(还真能丢。。。。。)那么此时如果使用EM算法,则贝耶斯分类器从有监督学习分类器变为了无监督学习的聚类器。
EM算法的优点是收敛迅速,每一步都需要使用充分统计。缺点是临近收敛时收敛速度下降。