之前谈到学习就是利用数据集对参数进行最大似然估计。本质上是获取一组有效的参数。然而如果考虑一个这样的问题：一枚硬币扔10次有7次朝上；扔1000次有700次朝上。显然对于二者而言，对参数的估计都是0.7。但是如果我们已知硬币是无偏的，那么第一次可以告诉自己是意外，第二次却很难说服。极大似然估计的问题是无法对先验知识进行建模并带入模型中。
1、贝叶斯估计
在极大似然估计中，我们使用的原理是使得theta = argmax P(x|theta)，这里theta作为一个确定的量。而贝叶斯估计的原理是 theta = max p(theta|x)，这里已经发生的 x 不再是随机变量，而theta 却被视作随机变量。如下图：
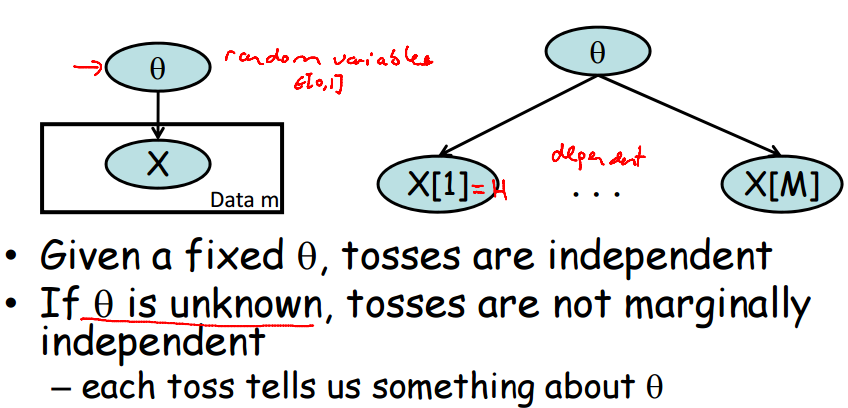
在theta作为随机变量的前提下，每一次的观测都会影响theta，toss之间并非独立（the trace is active）。
其中，P(theta|x[1],......x[M])是贝叶斯推断的核心方程。由于P(x[1],.....x[M])在贝叶斯推断中是以观测量，可通过联合概率密度函数边际化求取。换而言之，和theta没关系是个常数。所以这个核心方程就只和分子有关。分子又可以分为两部分，P(x[1]....x[M]|theta)是模型CPD，p(theta)称为先验概率，是我们对theta已知情况的猜测。
2、先验——狄利克雷分布
显然，初期对theta的假设（p(theta)）会对我们的最终结果有很大影响（同样对某人第一映像会对此人之后感觉有很大影响）。所以需要有个函数能够简明的来对先验分布进行建模，此函数就是狄利克雷函数。
从直觉上来说，狄利克雷函数里的参数alpha_k代表我们的先验观测。换言之，theta是服从多项分布的，第一项我们认为被观测到alpha_1次，第二项alpha_2次...
狄利克雷函数有个最好的性质：如果theta的先验分布是狄利克雷的，其CPD服从多项分布，那么theta的后验分布也是狄利克雷的。举个简单的例子，如果某个骰子，虽然是有偏的，但是假设无偏。开始实验且更新数据，那么这个过程是连续变化的。每一次的后验分布都是下一次的先验分布。并且，数字出现的次数是充分统计量。
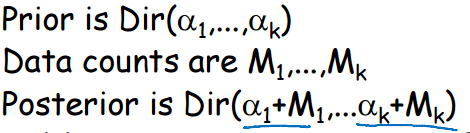
贝叶斯学习的本质是一种特殊的推断。因为此观点下，theta是随机变量。
3、贝叶斯预测
学习并估计参数的目的是进行预测。依据给定参数对变量发生的可能性进行预测如下式所示：
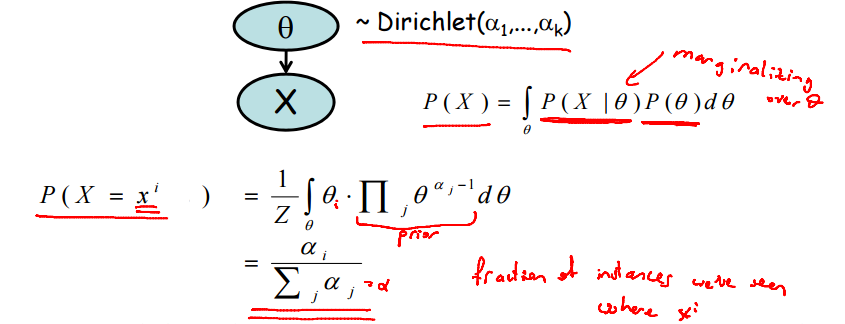
显然，先验概率代表之前发生的次数得到验证。
对于贝叶斯预测而言，在观测到M个变量后，只需要更新关于theta的先验分布即可。由充分统计可得，X[M+1]=xi的概率等于其频率。
4、在贝叶斯网络中使用贝叶斯估计
对于如图所示贝叶斯网络：
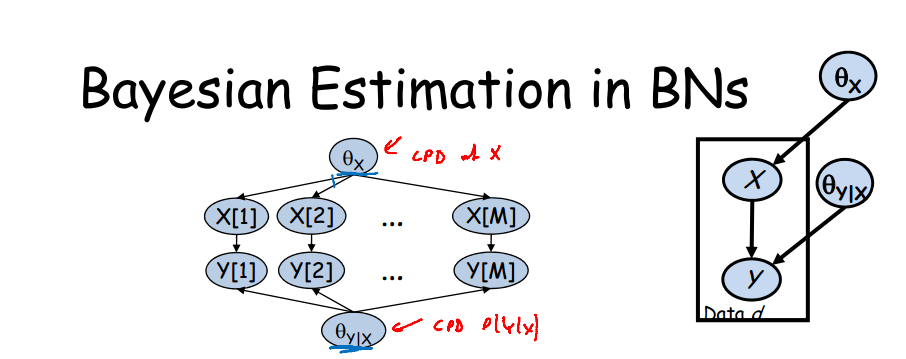
1、变量x[1]y[1]在给定参数的情况下与x[2]y[2]是独立的
2、参数theta_x,theta_xy在给定数据的情况下是独立的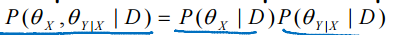
，所以，可以对两个P分别进行求解。
如果是狄利克雷先验情况下的多项式分布，那么关于theta的后验分布可以用充分统计的算法进行更新。
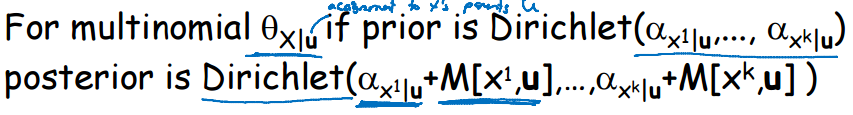
3、显然按照常理而言，如果要对网络中所有的参数设定先验分布，会是一件非常复杂的事情。theta_x 与 theta_y|x 需要匹配。因为theta_x 的狄利克雷分布具有“先验次数”的物理意义。故theta_y|x必须满足x的先验次数要求。
4、在设计好先验分布之后，则可用数据对先验分布进行更新。有先验分布的好处是数据能很快收敛。
总体而言，对于小样本数据，提供先验分布的方式可以防止数据发散。