基于采样的推理算法利用的思想是 概率 = 大样本下频率。故在获得图模型以及CPD的基础上,通过设计采样算法模拟事件发生过程,即可获得一系列事件(联合概率质量函数)的频率,从而达到inference的目的。
1、采样的做法
使用采样算法对概率图模型进行随机变量推理的前提是已经获得CPD。举个简单的例子,如果x = x1,x2,x3,x4的概率分别是a1,a2,a3,a4.则把一条线段分成a1,a2,a3,a4,之后使用Uniform采样,x落在1处,则随机变量取值为a1...依次类推,如图所示。
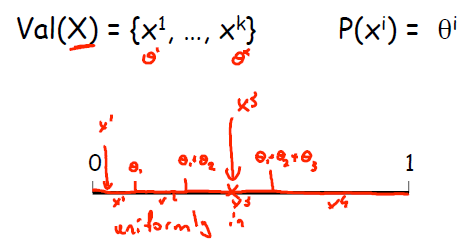
显然,采样算法中最重要的量就是采样的次数,该量会直接影响到结果的精度。关于采样次数有以下定理:

以简单的贝叶斯模型为例,如果最终关心的是联合概率,条件概率,单一变量的概率都可以使用采样算法。
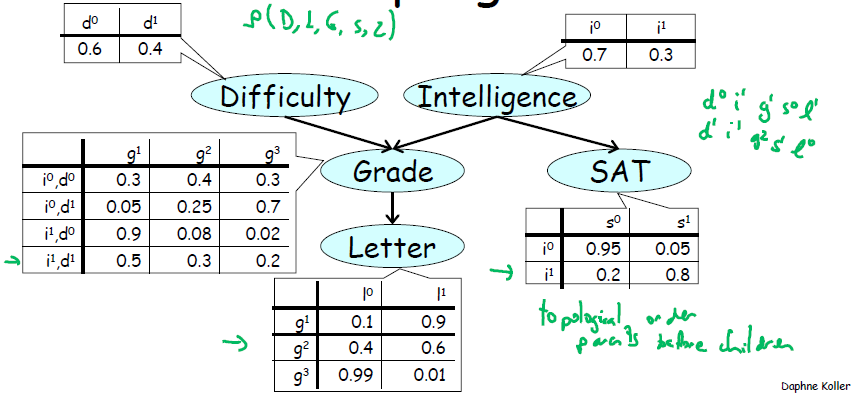
下图共需要设置 1+1+4+2+3 =11 个uniform采样器,最终得到N个结果组合(d0i1g1s0l1等)。最后计算每个组合出现的频率即可获得联合概率分布。通过边缘化则可获得单一变量概率。如果是条件概率,则去除最终结果并将符合条件的取出,重新归一化即可。
总结可知,采样算法有以下性质:
1.精度越高,结果越可靠,需要的采样次数也越多。
2.所关心的事件发生的概率很小,则需要很大的采样次数才能得到较为准确的结果。
3.如果随机变量的数量很多,则采样算法会非常复杂。故此算法不适用于随机变量很多的情况。
2、马尔科夫链与蒙特卡洛算法
马尔科夫链是一种时域动态模型,其描述的随机变量随着时间的推进,在不同状态上跳跃。实际上,不同的状态是随机变量所可能的取值,相邻状态之间是相关关系。引入马尔科夫链的目的是为了描述某些情况下,随机变量的分布无法用数学公式表达,而可利用马尔科夫链进行建模。把随机变量的取值视为状态,把随机变量视为跳蚤。马尔科夫链如下图所示:
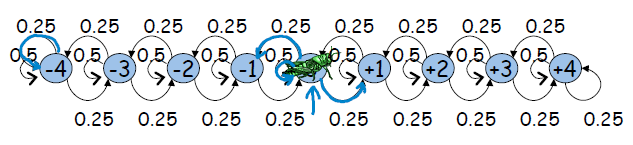

显然,对于简单的马尔科夫链我们大致还可以猜到或者通过方程解出CPD,但是一旦变量非常复杂,则我们很难获得CPD了。左图实际上是均匀分布,右图则可通过3元1次方程组对CPD进行求解。
马尔科夫链通过多次迭代后可以达到收敛的效果,如果要马尔科夫链收敛,则有以下两点要求:
1.马尔科夫链不允许有管进不管出的环
2.任何一个状态必须有回到自身的回路
3、使用马尔科夫链
使用马尔科夫链的前提是马尔科夫链已经收敛(mixed)。实际上,判断马尔科夫链迭代收敛是一件不可能的事情,而判断其未迭代收敛却是简单的。
1.对于马尔科夫链而言,蚱蜢落在相邻窗口的次数应该是相近的(因为总是在相邻窗口中跳跃)
2.蚱蜢从任意状态出发,最终收敛的结果应该是相近的。
一旦马尔科夫链迭代收敛,实际上我们得到了变量 x 的分布。
算法:
A<迭代收敛>
1. 选择不同的状态C个作为初始点(故有C条链)
2. 概率迭代T次(C条链同时进行)
3. 对比不同链条的相同窗口,观察次数是否相近
4. 假设马尔科夫链已经收敛
B<采样推理>
1.选择一个初始状态
2.依据转移概率计算所得采样
3.将所得采样放入采样结果集合中
4.利用采样结果集合计算所需要的量
4、Gibbs采样
之前以贝叶斯模型为例,展示了由叶向根的采样算法。然而概率图模型在实际使用中,往往使用马尔科夫模型或者混合模型。马尔科夫模型的有环特性使得其难以使用由叶向根的采样算法。Gibbs采样是一种简单快捷的采样方式,其可用于马尔科夫模型推理。其使用方法与贝叶斯模型的采样相同:
1.假设某个随机变量x1为未知,其他随机变量均为已知。
2.依据该条件下的概率P(x1|x-1),对未知随机变量x1进行采样
3.将采样结果迭代入下一次采样过程中
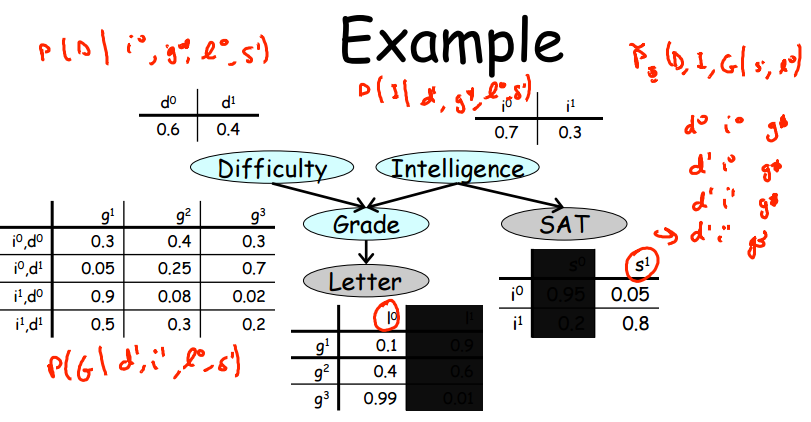
如图所示:如果已知L,S,则可假定D与I的值,对G进行采样,之后依据G的值重新对D进行采样。
这个思路听起来很简单,但是更致命的是这个算法实现起来也非常简单。

从图中可以看出,实际上采样的“核心”——条件概率值,仅仅和相邻的变量有关,而和图的整体无关!!!得到条件概率后丢进均匀分布采样即可。
5. Metropolis Hastings Algorithm
从上段可以看出,Gibbs采样算法是一种异常强大的算法,在构建MRF后,只要进行计算,就能够解出需要的概率。其缺点是面对难以发生的小概率事件需要多次迭代才能够收敛。考虑到此缺点,计算机科学家们设计了MH算法。这是一种在理论上就能保证收敛的算法。
该算法有一较强的约束条件,表现为下式:
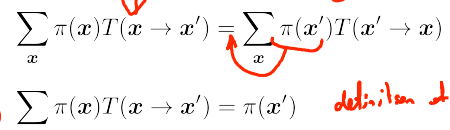
简而言之,就是随机变量转移到下个状态的可能性与其从下个状态转移回当前状态的可能性相等。马尔科夫链状态代表随机变量的取值,转移概率表示在当前状态下转移到下个状态的可能性。本算法则提出了更强的约束,在不破坏转移可能性的前提下,引入了状态发生概率的约束,来强行达到平衡。而这样约束所换取的好处就是某个随机变量的状态概率分布成了唯一的。(传统的马尔科夫链只要求T求和后等于1)
pi(x)是我们所求的目标。如何选择合适的T(x->x')就成了当前的主要任务。这里采用了一个很trick的方式来进行解释。

首先,由局部参数决定x',然后由"把关概率A"决定是否执行转移。A的设计有以下约束:
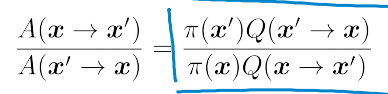
如果令A(x'->x) = 1, 则 A(x->x')=p.这是把关最松的情况,也就是让蚂蚱跳的尽可能快。
Q的设计据说是一份年薪65W美元的工作。。。
Q应该尽可能设计的扁平,也就是x转向x'的可能性要尽可能大,但是这会导致A变小...导致最终收敛变慢。
注:实际上,MH算法是提出了一种较强的约束,每个状态相互转移的可能性相同,而每个状态本身发生的可能性却可以是不同的。就像是人可以居住在城市不同的地方,如果你住的离学校近,那么你到学校的路就比较堵(转移的慢),如果你住的比较远,那么路可能更畅通(转移的快)人住的远近是随机变量没错,但是如果做出这种假设,人就有了更多选择的权利,远的地方有更大的可能性吸引人去居住。
6. 基于马尔科夫随机链蒙特卡洛算法的配对问题求解
配对问题本身是一个由MRF建模的问题,解铃还须系铃人,MRF引出的问题由MC来进行求解也算是一种循环吧。。。。。。

图示问题中,红点与蓝点进行匹配,一个红点有多个蓝点可以选择,其亲密程度由指数函数与抽象距离函数来进行描述。最终的目的是使得P(X1=v1,X2=v2....)达到最大。换一个思路来思考,假设红点和蓝点都是特殊的磁铁,红点会吸引蓝点,磁力和距离有关。如果采用MC的方法来进行求解,则每个红点是随机变量(5个磁力小球),蓝点是状态(8个铁块)。蒙特卡罗过程则是所有的磁力球一同落下,看看最终谁和谁吸在了一起。
如果用算法来描述一同落下就比较困难了,计算机科学家提出的算法如下:
1.随机变量与状态已经一一配准
2.某随机变量重新选择一个状态
3.被抢走配偶的随机变量选择状态
4.重复3直到平衡,作为一个结果
5.重复1~4,最后统计最可能发生的结果。
7、总结
从本质上来说,MRF是一种图模型,而MC是一种蒙特卡洛算法。MC可分为Gibbs Sample 以及MH 算法。Gibb Sample的难点在于不好收敛,MH算法的难点在于约束太强不好构造。