问题描述
在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
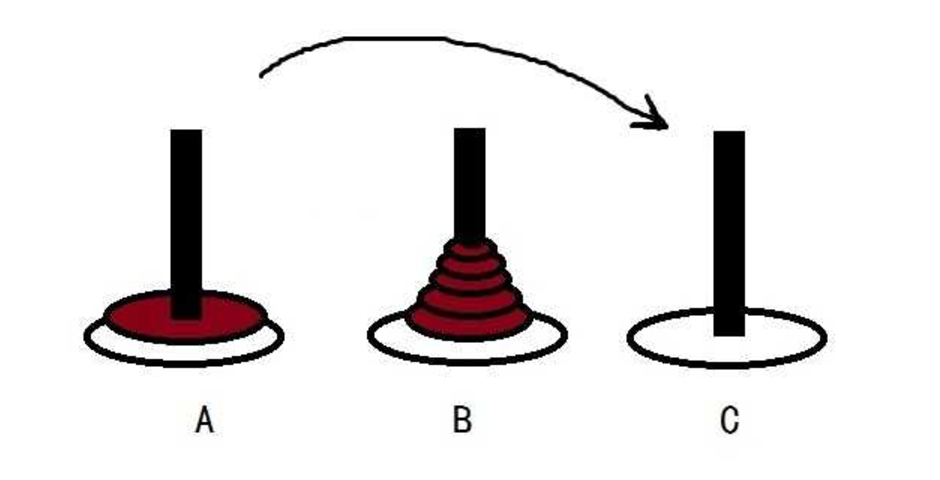
扯远了,把这个问题简单描述下有A,B,C三根柱子,将A柱上N个从小到大叠放的盘子移动到C柱,一次只能移动一个,不重复移动,小盘子必须在大盘子上面。
问一共需要移动多少次,步骤是什么?
解决思路
让我们从简单的情况下开始考虑
首先我说明几个数学符号,我自己瞎编的,为了方便表示问题,不用打那么多字
A -> B箭头意思代表是从 A柱 移动到 B柱 ,每次移动都是移动最上面的那一块
n = 1
- 只有一个盘子的时候,很简单,直接移就是了,用数学符号记录一下代表
A -> C
n = 2
- 如果有两个盘子,就分为三步
1.先将最上面的盘子也就是(从下往上数)第2个盘子,先移动到B 记为A -> B
2.然后将第一个盘子移动移动到C ,A -> C
3.最后将 B柱子上的盘子 移动到 C柱 ,B -> C
n = 3
- 如果有三个盘子,就分为7步,这里就不打字了,太累,用数学符号表示
A -> CA -> BC -> BA -> CB -> AB -> CA -> C

额,不要摆出一副黑人问号脸...,自己随便拿三个道具摆一摆就知道了
当你摆一摆的时候就知道,我知道了,一个盘子移动1次,二个盘子移动3次,三个盘子移动7次,四个盘子移动15次,N个盘子移动(2^n - 1)次!
恭喜你答对了!数学归纳法找规律不需多久就可以找到规律,但还有问题是究竟要怎么移呢?... 以及用程序怎么解决呢?
n = n....
抽象出这个问题
-
将问题抽象出来并且转化为数学模型或者公式,是解决现实生活中复杂问题的一个很好的解决办法,例如谷歌的翻译,大家都觉得很智能,自然语言的翻译从20世界60年代就开始研究了,具体细节这里不是重点,最后的解决思路是基于统计模型来解决的,也就是说,困扰了很多年的问题最后是抽象成一个概率论公式得以解决,事实上,众多复杂的问题最后进行抽象其实就是几个流程和公式而已,下面就以这个汉诺塔问题为例。
-
当有N个盘子的时候,似乎很难去想具体怎么实现,既然这么难想,就不用去想,首先这个问题,中有三个柱子,A,B,C,这里也太具体了,抽象一下,怎么抽象呢?假如这个问题只有2根柱子,你能完成吗?废话,肯定不行啊,我还需要一个柱子来辅助移动,所以这里的A,B,C三个柱子就抽象成,起始柱,中间柱,目标柱,这里用from,mid,to来表示
-
ok,现在是盘子的数量抽象成了n,柱子也抽象成了,from,mid,to 三种柱子,下面对过程进行抽象,将n个盘子从 from 柱子 移动到 to 柱 ,其实总体来看是三步
- 将n-1个盘子从 起始 柱 移动到 中间 柱
- 将第n个盘子从 起始 柱 移动到 目标 柱
- 将n-1个盘子从 中间 柱 移动到 目标 柱
这里你可能会说了,我靠,不是只让移动一个盘子的吗,你这第1步和第3步移动了n-1个盘子啊...,对,所以我这里的过程说的是抽象的过程,也就是说不管具体的实现细节是怎样的,要达成所有的盘子都从A->C的效果,中间一定是有一步是达到这个效果的,就好比你从北京去纽约,假设只有一条国际航班,要经过巴黎,那我就可以说你从北京去纽约,只有两步,第一步是去巴黎,第二步是从巴黎去纽约,这里的道理是同样的。
- 那么现在将上面的第1步怎么实现呢?同样抽象,只要将n 替换成 n-1 即可,第三步也是同理
- 将n-2个盘子从 起始 柱 移动到 中间 柱
- 将第n-1个盘子从 起始 柱 移动到 目标 柱
- 将n-2个盘子从 中间 柱 移动到 目标 柱
代码实现
那这个过程,用程序来抽象就是 一个Plate方法,接受四个参数,n,from,mid,to,四个参数的意思分别是
- n 代表要移动几个盘子
- from 代表起始柱的名字
- mid 代表借助的中间柱的名字
- to 代表目标柱的名字
方法的 作用是 将 n 个盘子 从 from 移动到 to
代码如下
/**
* 将n个盘子从 from 移动到 to
*/
public static void movePlate(int n, String from, String mid, String to) {
/* 如果只有一个盘子,就直接从 from 移动到 to */
if (n <= 1) {
System.out.println(from + " -> " + to);
return;
}
/* 1.将 n-1 个盘子 从 from 移动到 mid */
movePlate(n - 1, from, to, mid);
/* 2.将第 n 个盘子 从 from 移动到 to */
System.out.println(from + " -> " + to);
/* 3.将 n-1 个盘子 从mid 移动到 to */
movePlate(n - 1, mid, from, to);
}
你可以发现除去注释,真正的代码只有5行,就将这个问题给解决了,再次提醒这里的from , mid ,to 是形参,代表的是起始住,中间柱,和目标驻,不是具体的哪一个柱子,所以在第12行,因为第一步是将N-1个移动到中间柱,所以参数时from,to,mid,第18行将n-1个从中间柱移动到目标驻,所以参数时mid,from,to,中间的参数就是需要借助的柱子。
下面测试一下代码,这里根据题目把from,mid,to起个名分别是A,B,C,那执行这个方法就是将3个盘子从A移动到C
public static void main(String[] args) {
movePlate(3, "A", "B", "C");
}
n = 3 的时候
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
Process finished with exit code 0
发现和上面人为思考的结果是一样的哦
当n = 4的时候
A -> B
A -> C
B -> C
A -> B
C -> A
C -> B
A -> B
A -> C
B -> C
B -> A
C -> A
B -> C
A -> B
A -> C
B -> C
Process finished with exit code 0
一共是15步,也没有问题,再多的我就不测了,有兴趣的自己试试按照上面的打印结果来进行操作
推算次数
利用递归的方法同样可以很容易的写出计算次数的方法
public int countMovePlate(int n) {
if (n <= 1) return 1;
return countMovePlate(n - 1) + 1 +countMovePlate(n-1);
}
那问题来了,还能优化吗?
上文说到人为观察,利用数学归纳法可以得出需要的次数是 (2^n - 1) 次,那么这个数究竟是怎么得到呢?
先把上面的程序复制下来,进行观察
/* 1.将 n-1 个盘子 从 from 移动到 mid */
movePlate(n - 1, from, to, mid);
/* 2.将第 n 个盘子 从 from 移动到 to */
System.out.println(from + " -> " + to);
/* 3.将 n-1 个盘子 从mid 移动到 to */
movePlate(n - 1, mid, from, to);
核心代码就三行,假设moveplate这个方法需要移动的次数为(a_n)次,那么上面的这三行需要移动的次数就应该是$$ a_n = a_{n-1} + 1 + a_{n-1} $$
第一步是(a_n),第二步是固定的1次,第三步又是(a_n),然后当 n = 1的时候 (a_1 = 1) ,再总结整理一下就成了
有没有梦回高中的赶脚,这是一个很简单的变形等比数列,我们让两边都加上1
也就是
再提取一下
两边都除以 ((a_{n-1} + 1))
于是就成了
那接着将这个公式一直写竖式将他们相乘
接着约分,Markdown LaTex公式的删除线找了半天都没找到,知道的麻烦告知一下.
约分结果是
接着将前面的(a_1 = 1)代入,于是
再整理一下
所以说
将n =1 代入 n > 1 的情况,也是成立的,因此
所以经过推导之后java代码如下,因为涉及到(2^n)这种运算,可以使用移位符,这样底层移动速度很快
代码如下
public static int countMovePlate(int n) {
return n >= 1 ? (1 << n) - 1 : 0;
}
结论
最终我们解决汉诺塔的移动顺序与统计次数的代码如下,可以看出并不需要几行代码就解决了问题
/* 打印出移动顺序 */
public static void movePlate(int n, String from, String mid, String to) {
if (n <= 1) {
System.out.println(from + " -> " + to);
return;
}
movePlate(n - 1, from, to, mid);
System.out.println(from + " -> " + to);
movePlate(n - 1, mid, from, to);
}
/* 返回需要移动的次数 */
public static int countMovePlate(int n) { return n >= 1 ? (1 << n) - 1 : 0;}