1、关于图的表示
图G=(V,E),可以由两种数据结构进行表示,
一种表示方法是作为邻接链表的组合,另一种是使用邻接矩阵。
当然每一种表示方法适用的情景是不同的,
1.1 邻接链表表示法适用情形
稀疏图(变得条数远远小于点个数平方,即 |E|<<|V^2|)倾向于使用邻接链表对其进行表示。
优点是:邻接链表表示法的存储空间均可以达到O(V+E),数量级比较令人满意。
1.2 邻接矩阵表示法适用情形
稠密图:如果(|E|接近|V^2|),倾向于使用邻接矩阵对其进行表示。
如果希望可以在较短时间内就可以判断出两个点之间是否有边相连也是需要使用邻接矩阵来表示图的。
优点是:无论图中的边的个数达到多少,邻接矩阵的空间需求均是O(V^2),比较固定。
相比之下,邻接链表的空间需求具体是由图中点(V)和边(E)的个数来确定的。
2.基于图的搜索
2.1 广度优先搜索(BFS)
广度优先搜索是最简单的图搜索算法之一,基于BFS可以派生出来Prim最小生成树和Dijkstra的单源最短路径算法。
在给定一个图G=(V,E) 和一个可以识别的源结点s,调用广度优先算法可以实现从源节点s进行对整个图系统的搜索,
以得出从源点s到达图中所有可达结点的最短距离(也就是源点s与终点之间相隔的边数达到最少的情况)
广度优先算法的大致思想是:在搜索到所有的 距离源点s为k的点之后,才能继续往下扩展距离源点s距离为k+1的点。
广度优先算法的实现描述:
首先根据广度优先搜索过程构造出一棵广度优先树。
树的最初状态仅含有一个节点作为根节点也就是源点s。在扫描已发现节点u的邻接链表的时候(也就是点u已经被访问过,已经被收入到广度优先树中了),
每当发现一个未被访问节点v的时候,就将其点v和边(u,v)同时加入到树中。并且称u是v的前驱或是父结点,且v是u的后才。
在树中每个结点只有一个父节点。
为了方便描述,我们将结点设为{黑色,白色,灰色}三种颜色,
并且颜色作为结点的属性值分别代表该节点,{已经被扩展并且与之相连的所有结点都已经被扩展, 没有被扩展, 已经被扩展但是与之相连的结点没有被或是部分被扩展};
假定输入图G=(V,E)是以邻接链表所表示的。
该算法为图中每个结点赋予了一些额外的属性:
将每个结点u的颜色存放在属性u.color这个变量里面。
并且将u的前驱结点存放在属性u.f里面。如果u是没有前驱结点的,则设u.f=NIL.
u.d这个属性记录的是使用广度优先算法(BFS)所计算出来的从源点s到u之间的距离。
该算法使用一个先进先出的队列Q来管理灰色结点集。
下面是相关的伪码表示:
1 BFS(G,s) 2 //G is the graph and the s is the source point of the graph 3 4 for each vertex u attribute G.V -(s) 5 6 u.color = WHITE 7 8 u.d = MAX 9 10 u.f = NIL 11 12 //code above is initial every node's attributes 13 14 s.color = GRAY 15 16 s.f = NIL 17 //cause the s is the source , so if create a tree it must be the 18 //root of the tree ,so the root of s (s.f) is NIL 19 20 s.d = 0 21 //distance between source node s and itself is 0 22 23 s.front = NIL 24 25 Q = empty 26 27 ENQUEUE(Q,s) 28 29 while Q <> empty 30 31 u = DEQUEUE(Q) 32 33 for each v attribute to G.Adj[u] 34 //code describe v is a node that connect to node u 35 36 if v.color == WHITE 37 //the color of the node is WHITE illustrate that 38 //the node is unvisited 39 40 41 v.color = GRAY 42 //gray color illustrates the nodes of the node v is part visited 43 44 v.d = u.d +1 45 //there is a edge between v u two nodes 46 47 v.f = u 48 //u is the father node of v 49 50 ENQUEUE(Q, v) 51 52 53 //for circle end 54 55 u.color = BLACK 56 //cause after the circle all the nodes connect to node u 57 //are visited ,so the color of u is BLACK 58 59
下面是对伪代码的相应讲解:
4-10行,
是对所有的非源结点s的图结点的初始化过程,
执行一个循环:
在循环过程中,将所有的图中的非源结点的颜色属性值设为WHITE,代表的是并未对其进行访问过。
又将非源节点的各个结点的距离源节点的属性值d设置为无穷大。
并且在程序开始的时候,还没有对图进行扫描,所以并不知道每一个非源结点的父节点是哪一个,
所以将非源结点的代表前驱(即父结点)的属性值设置为NIL。
14-23行,
是对源结点s进行初始化操作。
将s的color属性设置为GRAY:表示的是,该结点已经被访问过,但是与之相邻的结点全部都没有被访问过或是部分被访问过。
接着将s的d属性值设置为0:表示的是,自己本身就是源结点,所以自己到自己的距离就是0
将s源结点的属性值f设置为NIL,表示的是,自己是源结点,但是就目前为止并不知道自己的前驱结点是哪一个所以置为空值。
25-最后:
首先将源点压栈,
然后进入到循环条件为栈Q不为空的循环中
首先出栈,然后访问出栈的结点对应的链表中的与之相连的后续元素,
(在这里我们将结点和元素区分一下:结点是指在邻接链表中的数组中的叫做结点,而该结点后续连接的叫做元素,
就拿下图来说吧,i对应的Adj中的值叫做结点,而i后续的k,s分别叫做元素,这里强调一下是因为,在具体实现的时候,二者的结构体类型会有相应的区别)
判断如果该元素的color属性值为WHITE那么说明这个结点并没有被访问过,因为这说明该结点在开始初始化color值被置成WHITE之后,就没有被修改过,所以就是没有被访问过。
接下来的访问操作对应的是针对该节点的
首先将该元素的color属性值更改为GRAY
然后将其与源点的距离d这个值置为当前结点的d值+1,
然后将这个元素的f值置成为该当前结点。
接下来,将当前元素放进队列中。
待到针对于当前结点(就是结点后续的所有元素都已经访问过后)
将当前结点的color属性置为BLACK,这是因为与之相连的所有点都已经被访问过了。
故置成BLACK
下面是实现上述伪码的代码,在这里LZ按照自己的理解对伪码进行表示。
因为仅考虑到算法过程的实现,所以并没有从全部图的数据结构出发对其进行实现。
也就是所并没有具体的表示该图的类型{有向图,无向图}
实现的具体数据结构请看下图:
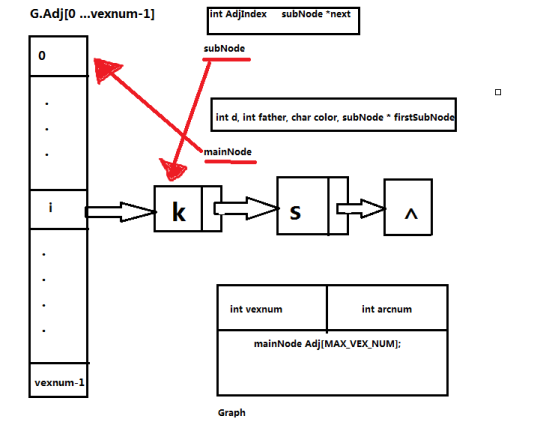
#include<stdio.h> #include<stdlib.h> #include<string.h> #include<queue.h> #define MAX_VEX_NUM 20
#define MAX_DIS -1 //使用-1来表示初始化的时候当前结点距离源点距离为无穷远
#define NIL NULL typedef struct subNode { int mainListLoc; struct subNode *next; }subNode; typedef struct mainNode { int d; char color[10]; int father; //this is not the pointer, it is the location the father node in the G.Adj[father] subNode *firstSubNode; }mainNode,mainNodeList[MAX_VEX_NUM]; typedef struct { int vexnum, arcnum; mainNodeList Adj; }Graph; //在这里并没有使用mainNode来表示源点,而是使用源点在邻接链表中的位序数值来表示
//同样也没有使用指针来表示一个点的前驱,而是使用int整型变量来表示它的父节点在邻接链表中的位序
void BFS_Graph(Graph G, int sourceNodeLoc) { queue<int> Q; int currentLoc; subNode *p; for(int i = 0; i < G.vexnum; i++) { if(i == sourceNodeLoc) { strcpy(G.Adj[i].color,"GRAY"); G.Adj[i].d = 0; G.Adj[i].father = -1; } else { strcpy(G.Adj[i].color,"WHITE"); G.Adj[i].d = MAX_DIS; G.Adj[i].father = -1; } } Q.push(sourceNodeLoc); while(!Q.empty()) { currentLoc = (int)Q.front(); p = G.Adj[currentLoc].firstSubNode; while(p!=NIL) { if(!strcmp(G.Adj[p->mainListLoc].color,"WHITE")) { strcpy(G.Adj[p->mainListLoc].color, "GRAY"); G.Adj[p->mainListLoc].d = G.Adj[currentLoc].d+1; G.Adj[p->mainListLoc].father = currentLoc; Q.push(p->mainListLoc); } p = p->next; } } strcpy(G.Adj[currentLoc].color,"BLACK"); }
BFS在ACM中主要用于求最短路径,
关于最短路径将会在下一篇中进行介绍。