PCA是一种非监督学习算法,它能够在保留大多数有用信息的情况下,有效降低数据纬度。
它主要应用在以下三个方面:
1. 提升算法速度
2. 压缩数据,减小内存、硬盘空间的消耗
3. 图示化数据,将高纬数据映射到2维或3维
总而言之,PCA干的事情就是完成一个将原始的n维数据转化到k维的映射。其中,k<n
它的核心算法如下:
1. 将数据均一化
x' = [x-mean(x)] / range(x)
2. 计算它的协方差矩阵
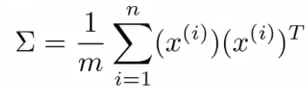
即:Sigma = 1/m * x' * x
3. 进行svd分解,计算特征向量
[U, S, V] = svd(Sigma)
选出U中的前k列,就可以得到映射公式啦
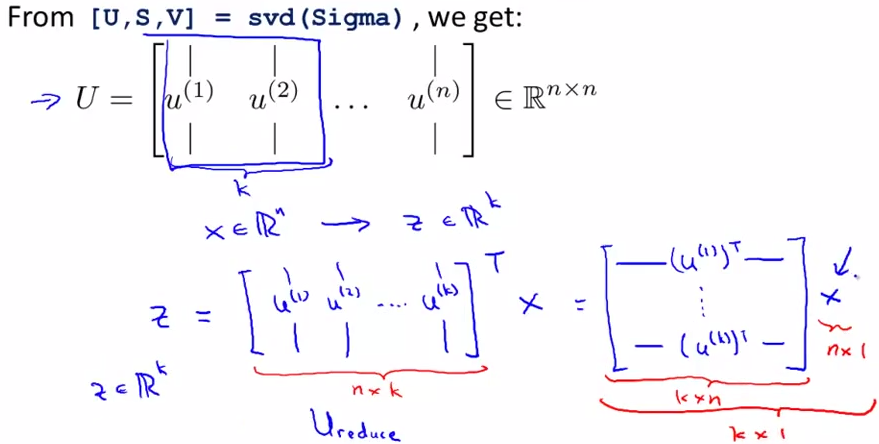
即:
Ureduce = U(:, 1:k);
z = Ureduce'*x;
其中,z便是降维后映射得到的特征矩阵。
至于如何选择k,那要看我们决定保留原始信息的多少变化范围(variance)。当我们想保留
原始信息99%的variance时:
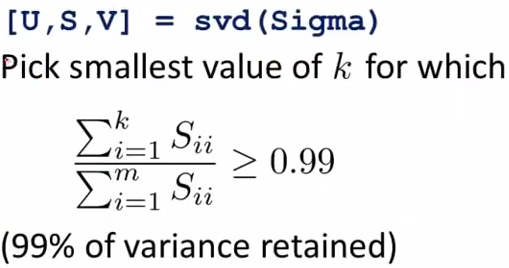
即:将S中前k个对角线元素相加,最小的能使相加和大于整个S的对角线和的99%的k便是我们应选择的k。
有压缩,那自然就有相应的还原。不过PCA本身的压缩是有损压缩,无法还原为与原来完全一样的值。(当然k=n另当别论)
我们只能够得到原始特征向量(非矩阵)的近似还原值。公式为:

即:Xapprox = Ureduce * Z
在使用PCA时,有几个要注意的地方:
1. 构建机器学习算法时,不要一上来就想要用PCA,一般而言,直接使用原始特征效果会比较好。
PCA是在原始算法过于缓慢,或者内存、硬盘空间实在不够大无法支撑计算时才有必要加入的
2. 不要用PCA来减小过拟合的问题,用regularization才是解决过拟合更为合理的方法。因为
PCA只看特征矩阵来决定如何减小特征数,而regularization同时看特征矩阵和对应的label来减小过拟合。