二叉树的常规遍历包括四种:前序、中序、后序和层序,其中前中后三种遍历均有递归和非递归形式。对这几种遍历方法进行改装,即可实现不同的功能。

二叉树的前序、中序、后序遍历过程可以这么理解:
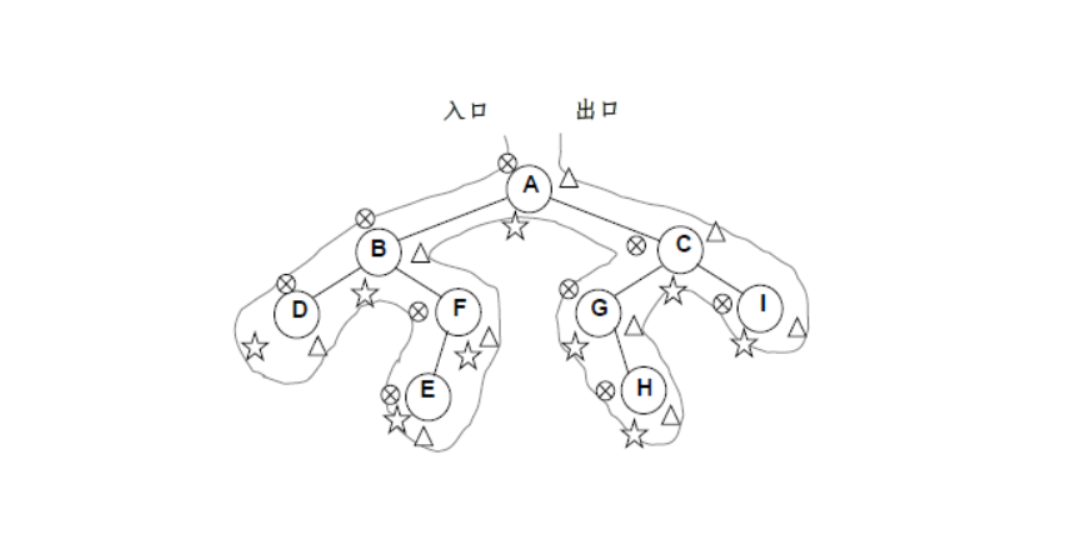
- 每一个结点都像一座城堡,每一个结点有三条边(没有儿子的结点也可以看成有两个指向空儿子的边),就像连接其他城堡的三堵墙;
- 一个人从根结点左侧入口处出发,沿着图示路线溜达一圈(不能穿墙),回到根结点右侧出口;
- 对于每一个结点城堡,这个人都会路过三次:第一次路过左侧,第二次路过下侧,第三次路过右侧;
- 这个人第一次路过时就进入城堡内部访问,则称为先序遍历,同理,第二第三次路过时访问就分别是中序遍历和后序遍历。
1 前序、中序、后序的递归形式
前序、中序、后序的递归形式非常简单,下面以中序遍历为例。
class Solution {
vector<int> ans;
public:
vector<int> inorderTraversal(TreeNode* root) {
if(root){
inorderTraversal(root->left); //遍历左子树
ans.push_back(root->val); //访问操作
inorderTraversal(root->right); //遍历右子树
}
return ans;
}
};
2 前序、中序的非递归形式
为了省去递归时多次调用函数的开销,可以自己维护一个堆栈。主要过程就是,持续地将左儿子压栈直至左儿子为空,然后弹出栈顶结点去看右儿子。以中序遍历为例(如果是前序遍历,压栈的时候就进行访问操作):
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> s;
TreeNode *T = root;
while(!s.empty() || T){
while(T){ //若结点非空,则一直将左儿子压栈
s.push(T);
T = T->left;
}
T = s.top();
s.pop();
ans.push_back(T->val); //访问操作
T = T->right;
}
return ans;
}
};
3 后序的非递归形式
后序的非递归形式和前序中序略有区别。主要原因是,压栈和出栈两个操作,刚好对应了第一次和第二次经过该结点;但后序遍历需要第三次经过该结点时再访问。所以在后序遍历中,堆栈中的结点不能直接出栈,需要先确认下是第二次经过还是第三次经过。因此可以再开一个栈,用以记录每个结点是否为第三次经过。
//对于每一个结点,压栈是第一次经过,瞄一眼发现没被标记过则是第二次经过,瞄一眼发现已经标记过一次则是第三次经过
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> s;
stack<bool> visited; //记录每个结点是否被瞄过
TreeNode* T = root;
while(T || !s.empty()){
while(T){
s.push(T);
visited.push(false); //将结点压栈的同时做个记录
T = T->left;
}
//瞄一眼栈顶结点,并检查是否之前被瞄过
T = s.top();
if(visited.top() == false){ //若未被瞄过,说明是第二次经过,则更新记录,转向右结点
visited.top() = true;
T = T->right;
}else{ //若已被瞄过,说明是第三次经过,则收进res中
ans.push_back(T->val);
s.pop();
visited.pop();
T = NULL; //避免T又被压栈
}
}
return ans;
}
};
4 层序遍历
前中后序遍历对应的是DFS的思想,而层序遍历对应的是BFS的思想。通常采用的方法是,利用一个队列,每次将一行结点拉出队时,顺便把它们的儿子结点塞进队。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(!root) return res; //排除空树
queue<TreeNode*> q;
TreeNode *T;
//开启循环
q.push(root);
while(!q.empty()){
int N = q.size(); //保存每一行的结点个数,起到了各层之间隔板的作用
vector<int> v; //保存这一行的结点值
while(N--){
T = q.front();
q.pop();
v.push_back(T->val);
if(T->left) q.push(T->left);
if(T->right) q.push(T->right);
}
res.push_back(v);
}
return res;
}
};
5 遍历的一些应用
求树的最大深度,最小深度;(层序遍历)
求树的右视图;(层序遍历)
锯齿层序遍历;(层序遍历的思想,但是利用两个栈来实现不同的方向)
叶节点个数;(几种遍历均可)
由前序遍历序列和中序遍历序列确定二叉树;(利用递归,过程同手动推导一样)
路径总和一二三;(递归形式)
其他应用待补充。。。